Kezdőlap


Feladat:	743. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alpár László , Busztin Ann , Farkas V. , Fröhlich K. , Gajzágó E. , Gyarmati B. , Nánássy Éva , Papp Zs. , Prém L. , Rácz I. , Varga Á. , Weiszfeld E.
Füzet:	1932/január, 132 - 133. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1931/november: 743. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $S$ a parabolák közös csúcsa, $t$ a megadott érintőjük és $F$ a parabolák egyikének gyújtópontja.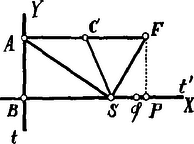

Ismeretes, hogyha a parabola gyújtópontjából valamely érintőre merőlegest állítunk, ennek talppontja a parabola csúcsérintőjén fekszik. Ha tehát

F

-ből

t

-re merőlegest állítunk és ennek talppontja

A

, akkor

A S

a parabola csúcsérintője és ez merőleges

S F

-re. Ha már most az

F

pont vetülete az

S

ponton át

t

-re állított merőleges

t'

egyenesen

P

, akkor

S F P ▵ \sim A S B ▵

(a szögek egyenlősége miatt) és így

\begin{matrix} F P : P S = S B : B A . \end{matrix}

Mivel

B A = F P

, az előbbi aránypárból:

{\bar{F P}}^{2} = \bar{B S} \cdot \bar{S P}

.
Eszerint az

F

pont mértani helye egy parabola, amelynek csúcsa az adott

S

pont, tengelye a

t

-re merőleges

t'

és paramétere

\frac{B S}{2}

. Ezen parabola gyújtópontja

φ

, a

t'

-n

\frac{B S}{4}

távolságban van az

S

ponttól.

Alpár László (izr. rg. VIII. o. Bp.)

Jegyzet. Legyen

C

A F

felezőpontja. Az

A S F

derékszögű háromszög, tehát

C S = A C

, azaz a

C

pont oly parabolát ír le, amelynek gyújtópontja

S

és vezérvonala

t

. Ha koordinátarendszerűnk

Y

-tengelye a

t

X

-tengelye a

t'

egyenes,

B S = a

, és a

C

pont koordinátái

x'

y

, akkor ezek között az

\begin{matrix} y^{2} = 2 a (x' - \frac{a}{2}) = a (2 x' - a) \end{matrix}

összefüggés áll fenn. Az

F

pont koordinátái

x = 2 x'

és

y

, tehát az

F

pont mértani helye az

\begin{matrix} y^{2} = a (x - a) \end{matrix}

parabola.