Feladat:	742. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. ,  Baneth L. ,  Blazsek I. ,  Braun J. ,  Busztin Anna ,  Csernussi E. ,  Csikós N. B. ,  Gajzágó E. ,  Gerber Zsuzsa ,  Gyarmati B. ,  Jónás J. ,  Kalán J. ,  Kálmán E. ,  Keztyüs I. ,  Kohner A. ,  Lehel P. ,  Meller P. ,  Mérei L. ,  Mitnyán L. ,  Nánássy Éva ,  Papp Zs. ,  Prém L. ,  Rácz I. ,  Réffy K. ,  Ritter G. ,  Róna I. ,  Róth Edith ,  Róth S. ,  Schilling M. ,  Schütz Gy. ,  Sohr Anna ,  Székely I. ,  Tarnóczy T. ,  Váradi L. ,  Varga Á. ,  Vezér György ,  Weiszfeld E.
Füzet:	1932/január, 131 - 132. oldal		PDF  |  MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Kör egyenlete, Osztópontok koordinátái, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1931/november: 742. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.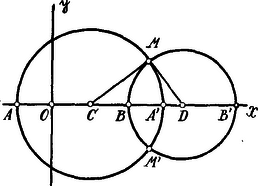   $1^{\circ }$. A feladatban foglalt kijelentésekből folyik, hogy az (1) és (2) egyenlet gyökei valósak és különbözök, tehát $\begin{array}{c}{\displaystyle b^2-4ac>0\text{és}b{\text{'}}^2-4a\text{'}c\text{'}>0.}\end{array}$ Feltehetjük még, hogy $a>0$ és $a\text{'}>0$. Ha már most az $A\text{'}$ pont abscissája $x_1$, az $A$ ponté $x_2$, akkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle \overline{AA\text{'}}=\overline{OA\text{'}}-\overline{OA}}\hfill \\ \hfill {\displaystyle x_1-x_2=\sqrt[]{{\left(x_1+x_2\right)}^2-4x_1{x}_2}=\sqrt[]{{\left(-\frac{b}{a}\right)}^2-4\frac{c}{a}}=\frac{\sqrt[]{b^2-4ac}}{a}\mathrm{.}}\hfill \end{array}}$ Hasonlóan $\begin{array}{c}{\displaystyle BB\text{'}=\frac{\sqrt[]{b\text{'}-4a\text{'}c\text{'}}}{a\text{'}}\mathrm{.}}\end{array}$ $2^{\circ }$. A $C$ pontra nézve $\begin{array}{c}{\displaystyle OC=\frac{x_1+x_2}{2}=-\frac{b}{2a}\mathrm{,}}\end{array}$ $\phantom{2^0\mathrm{.}}$ a $D$ pontra pedig: $\begin{array}{c}{\displaystyle OD=\frac{x{\text{'}}_1+x{\text{'}}_2}{2}=-\frac{b\text{'}}{2a\text{'}}\mathrm{.}}\end{array}$ $3^{\circ }$. Az $AA\text{'}$ és $BB\text{'}$ távolságok, mint átmérők fölött szerkesztett körök egyenletei: $\begin{array}{c}{\displaystyle {\left(x+\frac{b}{2a}\right)}^2+y^2=\frac{b^2-4ac}{4a^2}\mathrm{,}}\end{array}$ (3) ill. $\begin{array}{c}{\displaystyle {\left(x+\frac{b\text{'}}{2a\text{'}}\right)}^2+y^2=\frac{b{\text{'}}^2-4a\text{'}c\text{'}}{4a{\text{'}}^2}\mathrm{.}}\end{array}$ (4) A két kör metszéspontjainak koordinátai kielégítik a (3) és (4) egyenleteket; ha e két egyenlet megfelelő oldalain álló tagokat egymásból kivonjuk, lesz: $\begin{array}{c}{\displaystyle x=\frac{ac\text{'}-ca\text{'}}{ba\text{'}-ab\text{'}}\mathrm{,}}\end{array}$ azaz a két metszéspont ugyanazon abscissa által van meghatározva. Helyettesítsük $x$ ezen értékét a (3) és (4) egyenletek bármelyikébe, pl. a (3)-ba, megkapjuk az $M$ és $M\text{'}$ pontok ordinátáit, még pedig: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =\pm \sqrt[]{\frac{b^2-4ac}{4a^2}-{\left(\frac{ac\text{'}-ca\text{'}}{ba\text{'}-ab\text{'}}+\frac{b}{2a}\right)}^2}=\pm \frac{\sqrt[]{\left(ab\text{'}-ba\text{'}\right)\left(bc\text{'}-cb\text{'}\right)-{\left(ac\text{'}-ca\text{'}\right)}^2}}{ab\text{'}-ba\text{'}}\mathrm{.}}\hfill \end{array}}$ $4^{\circ }$. A cosinus-tétel alapján: $\text{cos}\widehat{CMD}=\frac{{\overline{MC}}^2+{\overline{MD}}^2-{\overline{CD}}^2}{2\overline{MC}\cdot \overline{MD}}$. Azonban: $MC=\frac{\sqrt[]{b^2-4ac}}{2a}$, $MD=\frac{\sqrt[]{b{\text{'}}^2-4a\text{'}c\text{'}}}{2a\text{'}}$, $CD=OD-OC=\frac{ab\text{'}-ba\text{'}}{2aa\text{'}}$. Helyettesítés és egyszerűsítés után: $\begin{array}{c}{\displaystyle \text{cos}\widehat{CMD}=\frac{bb\text{'}-2\left(ac\text{'}+a\text{'}c\right)}{\sqrt[]{\left(b^2-4ac\right)\left(b{\text{'}}^2-4a\text{'}c\text{'}\right)}}\mathrm{.}}\end{array}$ Vezér György (Dobó István r. VIII. o. Eger)