Kezdőlap


Feladat:	725. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Alpár L. , Busztin Anna , Gajzágó E. , Varga Á. , Weiszfeld E.
Füzet:	1931/november, 74. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1931/szeptember: 725. matematika feladat

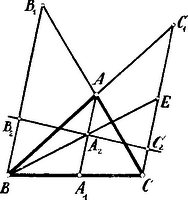
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $B$ csúcsot az $A_{2}$ -vel összekötő egyenes a $C C_{1}$ -t az $E$ pontban metszi.

B

csúcsból kiinduló sugársort

(B C, B E, B C_{1})

metszik az

A A_{1}

C C_{1}

párhuzamosak, tehát

\begin{matrix} \frac{\bar{A A_{2}}}{\bar{A A_{1}}} = \frac{\bar{C_{1} E}}{\bar{C_{1} C}} = \frac{\bar{E C_{1}}}{\bar{C C_{1}}} = \frac{\bar{C C_{1}} - (\bar{C C_{2}} + \bar{C_{2} E})}{\bar{C C_{1}}} = 1 - \frac{\bar{C C_{2}}}{\bar{C C_{1}}} - \frac{\bar{C_{2} E}}{\bar{C C_{1}}}, \end{matrix}

vagyis

\begin{matrix} \frac{\bar{A A_{2}}}{\bar{A A_{1}}} + \frac{\bar{C_{2} E}}{\bar{C C_{1}}} + \frac{\bar{C C_{2}}}{\bar{C C_{1}}} = 1. \end{matrix}

Ha kimutatjuk, hogy

\frac{\bar{C_{2} E}}{\bar{C C_{1}}} = \frac{\bar{B B_{2}}}{\bar{B B_{1}}}

, akkor a tételt igazoltuk. A párhuzamos szelőkre vonatkozó tételt ismételten alkalmazva:

\begin{matrix} \frac{\bar{C_{2} E}}{\bar{B_{2} B}} = \frac{\bar{A_{2} C_{2}}}{\bar{A_{2} B_{2}}} = \frac{\bar{A_{1} C}}{\bar{A_{1} B}} = \frac{\bar{A C_{1}}}{\bar{A B}} = \frac{\bar{C C_{1}}}{\bar{B_{1} B}}, \end{matrix}

tehát

\begin{matrix} \frac{\bar{C_{2} E}}{\bar{B B_{2}}} = \frac{\bar{C C_{1}}}{\bar{B B_{1}}}, \end{matrix}

azaz

\begin{matrix} \frac{\bar{C_{2} E}}{\bar{C C_{1}}} = \frac{\bar{B B_{2}}}{\bar{B B_{1}}} . \end{matrix}

Buszlin Anna (izr. leányg. VIII. o. Bp.)