Kezdőlap


Feladat:	706. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alpár L. , Blazsek I. , Gajzágó E. , Székely I. , Varga Á.
Füzet:	1931/október, 42 - 44. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Egyéb ponthalmazok a koordinátasíkon, Egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1931/május: 706. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A derékszögű koordináta-rendszer $X$ -tengelye legyen az $O A$ , az $Y$ tengelye az 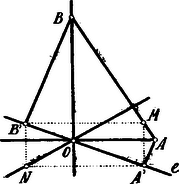$O B$ egyenes.

O

ponton át húzott tetszőleges egyenes egyenlete:

\begin{matrix} y = m x . \end{matrix}

(1)

Ezen egyenesre merőleges és az

A

ponton átmenő egyenes egyenlete:

\begin{matrix} y = - \frac{1}{m} (x - a) . \end{matrix}

(2)

B

ponton átmenő és az (1)-re merőleges egyenes egyenlete:

\begin{matrix} y - b = - \frac{1}{m} x ill. y = - \frac{1}{m} x + b . . \end{matrix}

(3)

Az (1) és (2) metszőpontja az

A'

; ennek koordinátái

\frac{a}{1 + m^{2}}, \frac{a m}{1 + m^{2}}

.
Az (1) ás (3) metszőpontja a

B'

ennek koordinátai:

\frac{b m}{1 + m^{2}}, \frac{b m^{2}}{1 + m^{2}}

.
Az

A'

ponton át az

Y

-tengellyel és a

B'

ponton át az

X

-tengellyel párhuzamos egyenes metszőpontja legyen

M

; ennek koordinátái tehát

\begin{matrix} x = \frac{a}{1 + m^{2}}, y = \frac{b m^{2}}{1 + m^{2}}; ezekre nézve : \frac{x}{a} + \frac{y}{b} = \frac{1 + m^{2}}{1 + m^{2}} = 1, \end{matrix}

(4)

azaz az

M

pont az

A B

egyenesen fekszik.
Az

A'

ponton át az

X

-tengellyel és a

B'

ponton át az

Y

-tengellyel párhuzamos egyenes metszőpontja legyen

N

; ennek koordinátái:

\begin{matrix} x = \frac{b m}{1 + m^{2}}, y = \frac{a m}{1 + m^{2}}; ezekre nézve : \frac{x}{b} - \frac{y}{a} = 0, \end{matrix}

(5)

azaz az

N

pont az origón átmenő és az

A B

-re merőleges egyenesen fekszik.

Jegyzet. A beérkezett megoldások ‐ egy kivételével ‐ azt állítják, hogy az

M

pont mértani helye az

A B

átfogót tartalmazó egyenes, az

N

ponté pedig az erre merőleges egyenes, mely az origón megy keresztül. A megoldásban ezen állítást módosítottuk, mert ezen egyenesek nem minden pontja lehet az

M

, ill.

N

pont. Legyen a szög, melyet az

e

egyenes az

O X

tengely pozitív irányával bezár,

φ

, tehát

m = tg φ

.
Az

M

pont koordinátái

\begin{matrix} x = \frac{a}{1 + m^{2}} = \frac{a}{1 + {tg}^{2} φ} = a cos^{2} φ; y = \frac{b m^{2}}{1 + m^{2}} = b {tg}^{2} φ cos^{2} φ = b sin^{2} φ . \end{matrix}

Mialatt

φ

változik

0^{0}

-tól

180^{\circ}

-ig,

x

értéke változik

a

-tól 0-ig, ezután 0-tól

a

-ig;

y

értéke pedig 0-tól

b

-ig, ezután

b

-től 0-ig, azaz: az

M

pont

A

-tól

B

-ig és

B

-től

A

-ig fut vissza, mialatt az

e

egyenes

180^{\circ}

-nyi forgást ír le (az

X

tengely poz. irányától számítva). Eszerint az

M

pont mértani helye az

A B

átfogó.
Az

N

pont koordinátái:

\begin{matrix} x = \frac{b m}{1 + m^{2}} = b tg φ cos^{2} φ = b sin φ cos φ = \frac{b sin 2 φ}{2}; y = \frac{a sin 2 φ}{2} . \end{matrix}

Mialatt

φ

változik

0^{0}

-tól

180^{\circ}

-ig,

\begin{matrix} \begin{matrix} x & változik & a & 0, & \frac{b}{2}, & 0, & - \frac{b}{2}, & 0 & értékek, \\ y & ,, & a & 0, & \frac{a}{2}, & 0, & - \frac{a}{2}, & 0 & érték között, \end{matrix} \end{matrix}

beleértve ezen határokat is. Eszerint az

N

pont az

O

ponton átmenő és

A B

-re merőleges egyenes azon szakaszán mozog, melynek határpontja a

\begin{matrix} (\frac{b}{2}, \frac{a}{2}) és (- \frac{b}{2}, - \frac{a}{2}) . \end{matrix}

koordináták által vannak meghatározva. Ezen határpontok akkor állanak elő, amikor

φ = 45^{\circ}

ill.

135^{\circ}

és távolságuk

O

-tól

= \frac{A B}{2}

.
Az itt jellemzett viszonyokat szemléltethetjük, ha meghúzzuk az

A O B ∢

felező egyenesét,

e_{1}

-t és az

O

ponton át az erre merőleges

e_{2}

-t. Az

A

pont vetülete az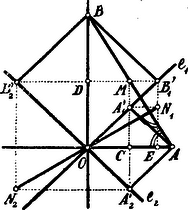

e_{1}

-n

A'_{1}

, a

B

ponté

B_{1}

O A A'_{1} ▵

és

O B B'_{1} ▵

egyenlőszárú háromszögek; ha tehát

A'_{1}

-ből

O A

-ra merőlegest állítunk, ez felezi

O A

-t a

C

pontban és ezért az

A B

-t is az

M

pontban és

A' C - \frac{O A}{2} = \frac{a}{2}

;

B'

-ből merőlegest állítva

O B

-re, ez felezi

O B

-t a

D

és

A B

-t az

M

pontban és

B' D = \frac{O B}{2} = \frac{b}{2}

. Húzzunk továbbá az

A'_{1}

; ponton át az

O A

-val, a

B'_{1}

; ponton át

O B

-vel párhuzamost; ezen két párhuzamos az

N_{1}

pontban metszi egymást; az

N_{1}

pont koordinátái:

O E = \frac{b}{2}

és

N_{1} E = \frac{a}{2}

. Kössük össze az

N_{1}

pontot

O

-val; az

O N_{1} E ▵ \sim B A O ▵

, mert a derékszöget bezáró oldalak aránya egyenlő és ezért

O N_{1} E ∢ = O A B ∢

. Ebből pedig következik, hogy

O N_{1} ⊥ A B

.
Ha az

A

pont vetülete az

e_{2}

-n

A'_{2}

, a

B

ponté

B'_{2}

, akkor ezekből kiindulva ugyanazon

M

ponthoz jutunk az

A B

-n, továbbá az

N_{2}

ponthoz úgy, hogy

O N_{2} ⊥ A B

.
Az

N

pont mértani helye az

N_{1} N_{2}

távolság oly módon, amint azt előbb jellemeztük. (Könnyen látható, hogyha az

e

egyenes az

e_{1}

vagy

e_{2}

helyzetéből elfordul, az

N

pont az

N_{1}

és

N_{2}

közé esik.)