Feladat: 671. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Albrecht J. ,  Alpár L. ,  Balassa Gy. ,  Baranyai K. ,  Bársony Stefánia ,  Barta F. ,  Budó Á. ,  Böszörményi M. ,  Emődi Gy. ,  Fejér Gy. ,  Gohn E. ,  Klein Béla ,  Kmoschek P. ,  Kohner A. ,  Kolhányi F. ,  Kövesdi D. ,  Lázár D. ,  Nay A. ,  Rosta F. ,  Sebők Gy. ,  Semmelweiss O. ,  Simon Á. ,  Singer Gy. ,  Singer I. ,  Szabó F. ,  Szabó I. ,  Szebasztián Rózsa ,  Székely I. 
Füzet: 1931/április, 247 - 248. oldal  PDF  |  MathML 
Témakör(ök): Számfogalom bővítése, Hiperbola egyenlete, Feladat
Hivatkozás(ok):Feladatok: 1931/február: 671. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen

z=x+yiész0=x-yi.z3-z03=(x3+3x2yi-3xy2-y3i)-(x3-3x2yi-3xy2+y3i)=(6x2y-2y3)i;z2-z02=(x2+2xyi-y2)-(x2-2xyi-y2)=4xyi;z-z0=2yi.


Az adott összefüggés
a(z3-z03)+b(z2-z02)+c(z-z0)=a(6x2y-2y3)i+4bxyi+2cyi=0
alakban írható. Ha y=0, akkor z=z0=x, azaz ekkor az adott egyenlet azonosság lesz (amelyet minden valós szám kielégít). Ezt, mint általános esetet kizárva, 2yi tényezőt eltávolíthatjuk és így
a(3x2-y2)+2bx+c=0(1)
összefüggéshez jutunk, amelyet valóban végtelen sok x, y értékpár elégít ki. Nevezetesen az (1)-ből
y2=3x2+2bax+ca.(2)
y2 az x minden értékénél pozitív, ha a (2) jobb oldalán álló másodfokú trinom discriminánsa <0, azaz
4b2a2-12ca=4(b2-3ac)a2<0,vagyisb2-3ac<0.

Ezen esetben x minden értékéhez két y érték tartozik, abszolút értékre egyenlő, de ellenkező előjelű. Más szóval: a (2) egyenletnek oly görbe felel meg, mely az X-tengelyre nézve két szimmetrikus ággal bír. Nyilván hiperbolával van dolgunk, melynek képzetes tengelye az X-tengel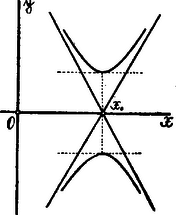y.
 
 

Ha b2-3ac>0, azaz a
3x2+2bax+ca=0egyenlet valós gyökeix1ésx2(x1<x2)
akkor
y2≥0,hax≤x1vagyx≥x2,
de
y2<0,hax1<x<x2.

Ezen esetben is az X-tengely szimmetria tengelye, de most valós tengelye a hiperbolának, melynek x1 és x2 között nincsenek pontjai.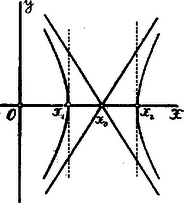
 
 

Ha b2-3ac=0, akkor a (2) baloldalán álló trinom teljes négyzet és a (2) egyenlet egy egyenespár egyenlete; t. i. c=b23a értékkel
y2=3(x+b3a)2,azaz[y+(x+b3a)3][y-(x+b3a)3]=0.

A két egyenes az X-tengely x0=-b3a pontjában metszi egymást; ez minden esetben a hiperbola középpontja. Irányhatározójuk: ±3; a két egyenes mindenkor a hiperbola egy-egy aszimptotája.
 

Klein Béla (Kölcsey Ferenc rg. VIII. o. Bp. VI.)