Kezdőlap


Feladat:	659. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Baranyai K. , Boros J. , Busztin Anna , Fejér Gy. , Gajzágó E. , Gohn E. , Hornyánszky I. , Kerekes S. , Klein B. , Kmoschek P. , Kohner A. , Kolhányi F. , Kövesdi D. , Lázár D. , Nay A. , Sebők Gy. , Simon Á. , Singer Gy. , Sohr Anna , Székely I. , Szendrő K. , Varga Á. , Weltzl J. , Zsemlye B. , Zsoldos P.
Füzet:	1931/március, 214 - 215. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1931/január: 659. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatban foglalt állítás akkor és csak akkor helyes, ha a két háromszög forgatással és párhuzamos eltolással fedésbe hozható.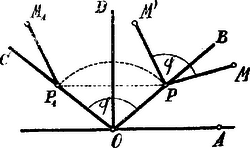
Hogy ezt világossá tegyük, a sík összes pontjait forgassuk el az $O$ pont körül $φ$ szöggel és azután vessük alá azokat az $\vec{O A}$ vektor által meghatározott transzlációnak. Kimutatjuk, hogy ekkor a síknak van egy ‐ és csakis egy ‐ $P$ pontja, amely a két művelet (transzformáció) után visszakerül a helyére, más szóval: a két transzformáció a $P$ pont helyzetét nem változtatta meg, míg minden más pont új helyzetbe került.

1^{\circ}

. Legyen

O D ⊥ O A

, a pozitív forgás irányában. Az

O B

és

O C

egyenesek az

O D

-re nézve szimmetrikus helyzetűek legyenek, úgy hogy

(O B, O C) = φ

, és

\vec{P_{1} P} = \vec{O A}

oly módon, hogy

P_{1}

O C

P

O B

egyenesen fekszik. Ekkor a sík pontjait az

O

körül

φ

szöggel elforgatva,

P

P_{1}

helyzetbe kerül; ha most a sík összes pontjait az

\vec{O A}

-val párhuzamosan és egyenlő mértékben eltoljuk, a

P_{1}

visszakerül

P

-be. Tehát a

P

pont a két transzformáció után megtartja eredeti helyzetét.

2^{\circ}

. A sík más pontja nem bírhat ezzel a tulajdonsággal; ugyanis ha volna még egy ilyen tulajdonsággal bíró

Q

pont, akkor a

P Q

egyenes is visszakerülne önmagára a két transzformáció után: ez azonban lehetetlen, mert a két transzformáció a sík minden egyenesének a helyzetét megváltoztatja.

3^{\circ}

. Az

1^{\circ}

. alatt leírt meghatározásból folyik, hogy a

P

pont az

O A

távolságot merőlegesen felező egyenesen fekszik.

4^{\circ}

. A két transzformáció helyettesíthető egy

P

pont körüli forgatással, melynek mértéke ugyancsak a

φ

szög.
Ugyanis: a tetszőleges

P M

vektort az

O

körüli forgatás

P_{1} M_{1}

helyzetbe, a

P_{1} M_{1}

-t az

\vec{O A}

transzláció a

P M'

helyzetbe hozza, azaz

P M

P M'

helyzetbe került a két művelet után és

(\bar{P M}, \bar{P M'}) = φ

5^{\circ}

. Ha tehát az

A B C ▵

valamely

φ

szögnek megfelelő forgatással és transzlációval az

A' B' C' ▵

helyzetébe hozható, van a síknak egy

P

pontja, amely körül az

A B C ▵

-et forgatva, ez az

A' B' C'

helyzetbe kerül; más szóval: a

P

pont egyenlő távolságba van

A

-tól és

A'

-től, ugyancsak egyenlő távolságban

B

-től és

B'

-től,

C

-től és

C'

-től, kell tehát, hogy az

A A'

-t,

B B'

-t,

C C'

-t merőlegesen felező egyenesek mindegyike a

P

ponton menjen keresztül. Másrészt a

4^{\circ}

. értelmében

\begin{matrix} (P A, P A') = (P B, P B') = (P C, P C') = φ, \end{matrix}

azaz

\begin{matrix} A P A' ∢ = B P B' ∢ = C P C' ∢ = φ . \end{matrix}

6^{\circ}

. Tegyük fel, hogy az

A B C ▵

és

A' B' C' ▵

az előbb említett két transzformációval nem hozható fedésbe; szerkesszük meg a

C'

pontnak az

A' B'

-re vonatkozó szimmetrikus pontját,

C''

-t; ekkor

A' B' C'' ▵ ≅ A B C ▵

és ezen két idomra nézve az

5^{\circ}

. alatt kimutatott tulajdonság fennáll, de az

A B C

és

A' B' C'

háromszögekre nézve már nem állhat fenn.

7^{\circ}

. Azon módon, amint a feladatban foglalt állítás háromszögekre érvényes, ugyanúgy érvényes két egybevágó sokszögre nézve is.

Szerk.