| Feladat: | 625. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Alpár L. , Baranyai K. , Faragó S. , Fejér Gy. , Kövesdi D. , Sebők György , Simon Á. , Weisz F. | ||
| Füzet: | 1930/december, 121. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Térgeometriai bizonyítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1930/október: 625. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A föltétel szerint -nak minden az -lel érintkező lapja nem megszakítás nélküli vonalban érintkezik -lel. Legyen -nak egy ilyen lapja az I, mely -lel pl. az élben és a csúcsban érintkezik. A felületnek van még olyan lapja, amely -nek és között valamelyik oldalán legalább egy élben érintkezik -lel, (mert hiszen és között vannak még élek, tehát megfelelő lapok is). Legyen egy ilyen lap a II., melynek egy, az és közötti éle . 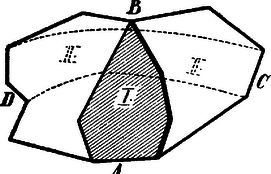 A föltétel szerint II. sem érintkezik az -lel folytonos vonalban és így két eset lehetséges: Vagy van a II. lapnak éle, ill. csúcsa az -nek és közötti másik (a -t nem tartozó) oldalán és ekkor az I. és II. lapnak már megvan a tételben kimondott tulajdonsága; vagy pedig a II. csak -nek az darabján függ össze -lel, de a föltétel szerint nem folytonos vonalban, hanem a és helyeken, melyek között van még egy idegen él, mondjuk a III. lapnak egy éle. Most tekintsük az határnak részét, mely legalább egy éllel kevesebb élt tartalmaz, mint és alkalmazzuk a II. és III. lapra ugyanazon meggondolást, mint előbb az I. és II. lapra: vagy felváltják egymást a II. és III.-nak az -lel való érintkezési helyei és akkor II. és III. bír a mondott tulajdonsággal, vagy pedig van a III. érintkezési helyei között egy IV. lapnak is éle s. í. t. Így minden egyes lépésnél legalább eggyel kevesebb élt tartalmazó határvonalra jutunk; mivel az élek száma véges, a kiválasztási eljárásunk egyszer befejeződik, mégpedig ha előbb nem találtuk meg a keresett két határlapot, akkor, amikor egy olyan -dik lapra jutunk, melynek -lel való és érintkezési helyei között csak egy él van s -hez tartozó -ik lap a határvonalon kívül is érintkezik egy csúcsban vagy élben az -lel. Az itt közölt megoldáshoz legközelebb áll Sebők Györgyé (Berzsenyi Dániel rg. VIII. o. Bp.). |