|
| Feladat: |
624. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Albrecht J. , Alpár L. , Baranyai K. , Barta F. , Deutsch E. , Deutsch I. , Faragó S. , Fejér Gy. , Gohn E. , Kemény I. , Klein B. , Kmoschek P. , Kövesdi D. , Mitnyán L. , Nay A. , Sebők Gy. , Simon Á. , Singer Gy. , Singer I. , Tóbiás I. , Vida L. , Weisz F. , Weltzl J. , Zsemlye Béla |
| Füzet: |
1930/december,
120. oldal |
 PDF | MathML |
| Témakör(ök): |
Síkgeometriai számítások trigonometria nélkül, Feladat |
| Hivatkozás(ok): | Feladatok: 1930/október: 624. matematika feladat |
|
|
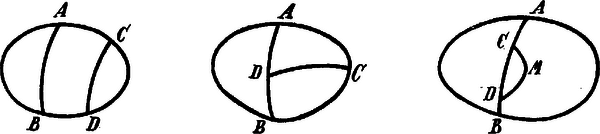
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelenleg csak az 1906 december előtt vagy az 1937 január és 2021 december között megjelent szövegeket tudjuk megjeleníteni. Kérjük, írjon az archiv@komal.hu e-mail címre, ha szüksége van a szövegre. |
|