Kezdőlap


Feladat:	618. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Albrecht J. , Alpár L. , Balassa Gy. , Bársony S. , Barta F. , Boros János , Budó Ágoston , Deckner G. , Dénes P. , Erdős L. , Ernszt F. , Fejér Gy. , Gohn E. , Grünsfeld M. , Hollay F. , Jónás J. , Kemény I. , Klein B. , Kmoschek P. , Kolhányi F. , Kovács J. , Kövesdi D. , Marcsa M. , Nay A. , Parti I. , Parti L. , Pongrácz Gy. , Popper Gy. , Ritter G. , Róna I. , Scholcz G. , Sebők Gy. , Semmelweiss O. , Simon Á. , Singer Gy. , Singer I. , Stekler E. , Szabó F. , Székely I. , Tóbiás I. , Vezér Gy. , Weisz F. , Weltzl J. , Zsemlye B.
Füzet:	1930/december, 114 - 115. oldal		PDF \| MathML
Témakör(ök):	Feladat
Hivatkozás(ok):	Feladatok: 1930/október: 618. matematika feladat

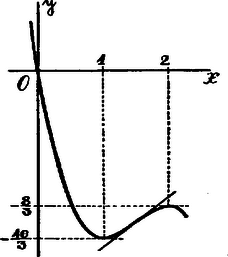
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az

\begin{matrix} y = a x^{3} + b x^{2} + c x + d \end{matrix}

függvény értéke az

x = 0

helyen zérus, akkor

d = 0

; így az

a

b

c

együtthatókat kell még meghatároznunk. Az

x = 1

helyen a függvény értéke

\begin{matrix} a + b + c = - \frac{10}{3} . \end{matrix}

(1)

\begin{matrix} y = a x^{3} + b x^{2} + c x \end{matrix}

függvény szélső értékei az

\begin{matrix} y' = 3 a x^{2} + 2 b x + c = 0 \end{matrix}

(2)

egyenlet által meghatározott

x

értékek mellett állanak elő; adataink szerint tehát a (2) egyenlet gyökei

x = 1

és

x = 2

, azaz

\begin{matrix} - \frac{2 b}{3 a} = 2 + 1 = 3, & (3) \\ \frac{c}{3 a} = 2 \cdot 1 = 2. & (4) \end{matrix}

(3)-ból

b = - \frac{9 a}{2}

; (4)-ből

c = 6 a

. Ezeket (1)-be helyettesítve:

\begin{matrix} a - \frac{9 a}{2} + 6 a = - \frac{10}{3} és innen a = - \frac{4}{3}; b = 6; c = - 8. \end{matrix}

A keresett függvény eszerint

\begin{matrix} y = - \frac{4}{3} x^{3} + 6 x^{3} - 8 x . \end{matrix}

Ennek változását a köv. táblázat tünteti fel:

\begin{matrix} x \end{matrix}