Kezdőlap


Feladat:	612. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Albrecht J. , Alpár László , Bakay B. , Balassa Gy. , Barta F. , Busztin Anna , Ernst F. , Fejér Gy. , Gajzágó E. , Klein B. , Kolhányi F. , Kövesdi D. , Lázár D. , Nay A. , Sebők György , Semmelweiss O. , Simon Ágoston , Singer Gy. , Singer I. , Szebasztián Rózsa , Tóbiás I. , Weisz Fülöp , Weisz K. , Weltzl J. , Zsemlye B.
Füzet:	1930/november, 88 - 90. oldal		PDF \| MathML
Témakör(ök):	Feuerbach-kör, Feladat
Hivatkozás(ok):	Feladatok: 1930/szeptember: 612. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A $B B_{1}$ oldalfelező középpontja legyen $B'$ , a $C C_{1}$ -é $C'$ ; a két oldalfelező metszőpontja $S$ , (a háromszög súlypontja).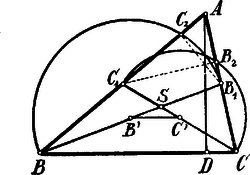

Így

\begin{matrix} S B' = S B - B B' = S B - \frac{1}{2} B B_{1} = S B - \frac{1}{2} \cdot \frac{3}{2} S B = \frac{1}{4} S B . \end{matrix}

Hasonlóan

S C' = \frac{1}{4} S C

, tehát

\begin{matrix} S B' : S B = S C' : S C \end{matrix}

és ezért

B' C' ∥ B C

. Ebből következik, hogy az

A

csúcsból vont magasság merőleges

B' C'

-re, a szóban forgó két kör centrálisára. Ha még kimutatjuk, hogy az

A

pont hatványa a két körre nézve egyenlő, akkor a tétel igaz.
A

B B_{1}

átmérő fölött szerkesztett kör az

A B

oldalt messe

C_{2}

-ben, tehát

B_{1} C_{2} ⊥ A B

és ezért

B_{1} C_{2} = \frac{1}{2} m_{c}

(a háromszögnek az

A B

oldalhoz tartozó magassága.)
A

C C_{1}

átmérő fölött szerkesztett kör az

A C

oldalt messe

B_{2}

-ben, tehát

C_{1} B_{2} ⊥ A C

és így

C_{1} B_{2} = \frac{1}{2} m_{b}

. ¹
Minthogy

A C_{1} B_{2} ▵ \sim A B_{1} C_{2} ▵

, ²

\begin{matrix} \frac{A C_{2}}{A B_{2}} = \frac{B_{1} C_{2}}{C_{1} B_{2}} = \frac{m_{c}}{m_{b}} = \frac{A C}{A B} tehát \bar{A B} \cdot \bar{A C_{2}} = \bar{A C} \cdot \bar{A B_{2}} . \end{matrix}

Ezen egyenlet kifejezi azt, hogy az

A

pont hatványa mindegyik körre nézve ugyanakkora.

Weisz Fülöp (izr. rg. VIII. o. Bp.)

II. Megoldás. Az

A

csúcsból vont magasság, mint láttuk, merőleges a

B' C'

centrálisra. Kimutatjuk még, hogy a magassági pont hatványa a szóban forgó két körre nézve egyenlő.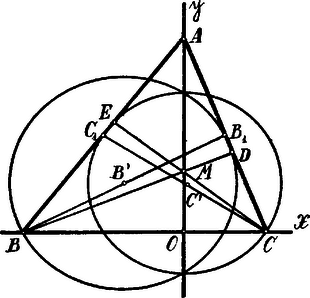

B B_{1}

oldalfelező, mint átmérő fölött szerkesztett kör az

A C

oldalt a

B

csúcsból vont magasság

D

talppontjában, a

C C_{1}

-hez tartozó kör az

A B

oldalt a

C

csúcsból vont magasság

E

talppontjában metszi. Ha a magassági pont

M

, akkor szögeik egyenlősége miatt

\begin{matrix} B M E ▵ \sim C M D ▵, \end{matrix}

tehát

\begin{matrix} M B : M C = M E : M D, \end{matrix}

vagyis

\begin{matrix} \bar{M B} \cdot \bar{M D} = \bar{M C} \cdot \bar{M D} \end{matrix}

azaz az

M

pontnak mindkét körre vonatkozó hatványa egyenlő és ezért, tekintettel arra, hogy

A M ⊥ B' C'

, az

A M

magassági vonal a két kör hatványvonala.

Alpár László (izr. rg. VII. o. Bp.)

III. Megoldás. A háromszög Feuerbach köre keresztülmegy az előbbi megoldásban meghatározott

B_{1}

D

C_{1}

E

pontokon. Eszerint a Feuerbach-kör és a

B'

középpontú kör hatványvonala a

B_{1} D \equiv A C

egyenes; a Feuerbach-kör és a

C'

középpontú kör hatványvonala a

C_{1} E \equiv A B

egyenes. Ebből következik, hogy a

B'

és

C'

körök hatványvonala az

A

ponton megy keresztül. E hatványvonalnak merőlegesnek kell lennie a

B' C'

centrálisra és így a vele párhuzamos

B C

oldalra, tehát nem más, mint az

A B C ▵

-nek

A

csúcsból vont magassága.

Sebők György (Berzsenyi Dániel rg. VIII. o. Bp. V.)

IV. Megoldás. Vegyük fel a derékszögű koordináta rendszert úgy, hogy a

B C

oldal az

X

-tengelyen, az

A

csúcs az

Y

-tengelyen feküdjék. A csúcspontok koordinátái legyenek:

\begin{matrix} A : (0, m), B : (b, 0), C (c, 0) . \end{matrix}

\begin{matrix} A B_{1} & pont & koordinátái & : & (\frac{c}{2}, \frac{m}{2}); & a C_{1} ponté & : & (\frac{b}{2}, \frac{m}{2}) . \\ A B' & ,, & ,, & : & (\frac{2 b + c}{4}, \frac{m}{4}); & a C',, & : & (\frac{b + 2 c}{4}, \frac{m}{4}) . \end{matrix}

B'

kör sugarának négyzete:

\begin{matrix} {\bar{B B'}}^{2} = r_{1}^{2} = {(\frac{2 b + c}{4} - b)}^{2} + \frac{m^{2}}{16} = \frac{{(c - 2 b)}^{2} + m^{2}}{16} . \end{matrix}

C'

kör sugarának négyzete:

\begin{matrix} {\bar{C C'}}^{2} = r_{2}^{2} = {(\frac{b + 2 c}{4} - c)}^{2} + \frac{m^{2}}{16} = \frac{{(b - 2 c)}^{2} + m^{2}}{16} . \end{matrix}

A két kör hatványvonalának egyenletét megkapjuk, ha a két kör zérusra redukált egyenleteinek baloldalait egyenlővé tesszük, tehát:

\begin{matrix} {(x - \frac{2 b + c}{4})}^{2} + {(y - \frac{m}{4})}^{2} - \frac{{(c - 2 b)}^{2} + m^{2}}{16} = \\ = {(x - \frac{b + 2 c}{4})}^{2} + {(y - \frac{m}{4})}^{2} - \frac{{(b - 2 c)}^{2} + m^{2}}{16} . \end{matrix}

A kijelölt műveletek végrehajtása és összevonás után

\begin{matrix} (b - c) x = 0 \end{matrix}

egyenlethez jutunk. Minthogy

b - c \neq 0

, a hatványvonal egyenlete

x = 0

, azaz a hatványvonal az

Y

-tengely, az

A B C ▵

-nek az

A

csúcsából vont magassági vonala.

Simon Ágoston (Berzsenyi Dániel rg. VIII. o. Bp.)

B_{1} C_{2}

C_{1} B_{2}

A B_{1} C_{1} ▵

magasságvonalai, az

A

-ból húzott magassági vonalon metszik egymást.

²Mind a kettő derékszögű és az $A$ csúcsnál közös szögük van.