Feladat: 599. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Alpár L. ,  Balassa Gy. ,  Déman P. ,  Erdős Pál ,  Fejér Gy. ,  Grünwald Tibor ,  Kövesdi D. ,  Sebők Gy. ,  Szebasztián Rózsa ,  Weisz F. 
Füzet: 1930/október, 55 - 56. oldal  PDF  |  MathML 
Témakör(ök): Feladat
Hivatkozás(ok):Feladatok: 1930/május: 599. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen OP⊥PX≡m. A P pontból húzott érintők érintési pontjai A és B. A PA érintő az egymásra merőleges d ill. d' átmérőt a K ill. M, a PB érintő L ill. N pontban metszi. Az LM és KN egyenesek metszőpontja legyen R; bebizonyítandó, hogy az R pont a PX≡m egyenesen fekszik, vagyis, hogy az LM, KN és PX egyenesek egy ponton mennek keresztül.
A P pontnak a K körre vonatkozó polárisa az AB egyenes; az m egyenes pólusa az AB-n fekszik, mégpedig az AB felezőpontja E.
Az M pont polárisa az A érintési pontból az OM átmérőre állított e merőleges; az L pont polárisa a B (érintési) pontból az OL átmérőre vont f' merőleges. Így az LM egyenes pólusa az e és f' egyenesek közös pontja C.
A K pont polárisa az A pontból az OK átmérőre merőleges f, az N ponté pedig a B ponttól az ON átmérőre merőleges e' egyenes; tehát a KN egyenes pólusa az f és e' egyenesek közös pontja D.
Az e, e', f, f' egyenesek, melyek páronként a d és d' egymásra merőleges átmérőkkel párhuzamosak, egy téglalapot határoznak meg: ACBD-t. Az E az AB átló felezőpontja; ezen keresztül megy a CD átló is, azaz: a C, D, E pontok egy egyenesen feküsznek és így a polárisaik, az LM, KN és PX egyenesek egy ponton mennek keresztül!

 

Erdős Pál (Szent István rg. VIII. o. Bp.)

 

 

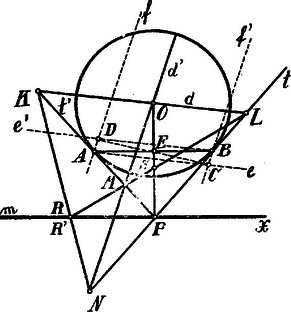II. Megoldás. A P pontból húzott t és t' érintők szögét PO felezi, minthogy PO⊥m, a t, t', PO és m egyenesek harmonikus sugárpárt alkotnak; ezen sugárpárt az LM egyenes az L, M és S, R harmonikus pontpárokban metszi, azaz a négy pont kettős viszonya:
(LMSR)=-1.(1)

Másrészt a d, d' átmérők és a t, t' érintők teljes négyoldalt határoznak meg, melynek átlói az LM, OP, KN egyenesek. Ha már most az LM átló, mely az OP-t az S pontban, a KN átlót az R' pontban metszi, akkor
(LMSR')=-1.(2)
(1)-ből és (2)-ből következik, hogy
R'≡R.

Kimondhatjuk egyszersmind, hogy a d és d' átmérőknek nem kell egymásra merőlegeseknek lenniük!
 

Grünwald Tibor (Br. Eötvös József r. VIII. o. Bp.)
 

III. Megoldás. Legyen az m≡PX egyenes a koordináta-rendszer X tengelye, PO az Y tengelye. A P pontból húzott érintők egyenletei:
y=kx,(1)
ill.
y=-kx.(2)

Az O ponton, (0,b) átmenő átmérők egyenlete:
y=rx+b,(3)
ill.
y=sx+b.(4)

A K pont koordinátai: (2)-ből és (3)-ból:
XK=-bk+r,YK=kbk+r.

A L pont koordinátai: (1)-ből és (3)-ból:
XL=bk-r,YL=kbk-r.

A M pont koordinátai: (2)-ből és (4)-ből:
XM=-bk+s,YM=kbk+s.

A N pont koordinátai: (1)-ből és (4)-ből:
XN=bk-s,YN=kbk-s.

Az LM egyenes egyenlete:
|xy1bk-rkbk-r1-bk+skbk+s1|=0.(5)

A KN egyenes egyenlete:
|xy1-bk+rkbk+r1bk-skbk-s1|=0.(6)

Mind a két egyenes egyenletéből:, ha y=0, x=-2br+s, tehát mindkét egyenes az X-tengelyt ugyanazon pontban metszi.
 

Grünwald Tibor (Br. Eötvös József r. VIII. o. Bp.)
 

Jegyzet: A megoldás azt mutatja, hogy az O ponton át húzott átmérőknek nem kell egymásra merőlegesnek lenniük; továbbá, hogy az R ponthelyzete független a kör sugarától, vagyis a P pontból húzott érintők irányától.