Kezdőlap


Feladat:	579. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Barna I. , Barok Gy. , Barta F. , Beke I. , Budó Ágoston , Busztin Anna , Böszörményi M. , Déman P. , Déry E. , Epstein T. , Erdős Pál , Ernst F. , Faragó T. , Fejér Gy. , Feldheim E. , Gillemot L. , Gohn Emil , Grünwald T. , Jakobovits J. , Jánosi S. , Kiss Gy. , Klein B. , Kmoschek P. , Kolhányi F. , Kövesdi D. , Ligeti M. , Löw A. , Marthé F. , Molnár D. , Nay A. , Papp Gy. , Raisz I. , Scheibner K. , Schossberger A. , Sebők Gy. , Semmelweiss O. , Simon Á. , Singer Gy. , Somló T. , Soos G. , Stern M. , Straubert J. , Szebasztián Rózsa , Székely I. , Varga T. , Vida L. , Vincze I. , Waldhauser Ilona , Weisz F.
Füzet:	1930/május, 290 - 291. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Egyenes körkúpok, Terület, felszín, Síkgeometriai számítások trigonometria nélkül körökben, Feladat
Hivatkozás(ok):	Feladatok: 1930/március: 579. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Az $A B$ átmérővel legyen párhuzamos az $M P Q N$ húr, amely az $A B C ▵$ $C O$ magassága körül forgatva, leírja a kúp alapkörével párhuzamos síkot.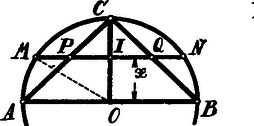

Ezen sík a gömböt az

M I

, a kúpot a

P I

sugarú körben metszi. Így

\begin{matrix} {\bar{M I}}^{2} = {\bar{O M}}^{2} - {\bar{O I}}^{2} = R^{2} - x^{2} és P I = C I = R - x . \end{matrix}

A gömbmetszet területe:

(R^{2} - x^{2}) π

;

\begin{matrix} a kúpmetszeté: {(R - x)}^{2} π . \end{matrix}

A feladat követelménye:

\begin{matrix} (R^{2} - x^{2}) π - {(R - x)}^{2} π = a^{2} π \end{matrix}

vagyis

\begin{matrix} 2 x^{2} - 2 R x + a^{2} = 0. \end{matrix}

(1)

Az (1) egyenletnek valósak a gyökei, ha

\begin{matrix} 4 R^{2} - 8 a^{2} ≧ 0, tehát a ≦ \frac{R \sqrt[]{2}}{2} . \end{matrix}

(2)

Ha a gyökök valósak, mind a kettő pozitív és mivel összegük:

R

, egyik sem lehet

R

-nél nagyobb. Eszerint az

\begin{matrix} x_{1,2} = \frac{R \pm \sqrt[]{R^{2} - 2 a^{2}}}{2} \end{matrix}

értékek mindegyike megfelel.

\begin{matrix} Ha a = \frac{R \sqrt[]{2}}{2}, akkor a két gyök egyenlő: x_{1} = x_{2} = \frac{R}{2} . \end{matrix}

2^{\circ}

. A szóban forgó két kör területének különbsége:

\begin{matrix} y = (R^{2} - x^{2}) π - {(R - x)}^{2} π = (- x^{2} + R x) 2 π . \end{matrix}

Ezen függvény folytonos és értéke zérus, ha

x = 0

és

x = R

.
A függvénynek maximuma van, ha

x = \frac{R}{2}

.
A függvény változását a köv. táblázat mutatja:

\begin{matrix} x & 0 & \frac{R}{2} & R \\ y & 0 & ↗ & \frac{R^{2} π}{2} & ↘ & 0 \\ Max. \end{matrix}

Gohn Emil (Koháry István rg. VII. o. Gyöngyös)