Feladat: 521. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Barok György ,  Csiky János ,  Déman P. ,  Fekete F. ,  Grünwald Tibor ,  Kövesdi D. ,  Liebermann J. ,  Ligeti M. ,  Sámuel J. ,  Simon Á. ,  Soos G. ,  Straubert J. 
Füzet: 1929/december, 120. oldal  PDF  |  MathML 
Témakör(ök): Inverzió, Diszkusszió, Körérintési szerkesztések, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1929/október: 521. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen az inverzió pólusa az A pont és modulusa az A pontnak k körre vonatkozó hatványa. Így a k inverze maga a k kör; az e egyenes inverziója oly kör, mely az A ponton megy keresztül. A keresett kör inverziója azonban egyenes, mely az e inverzióját érinti és a k-t merőlegesen metszi, azaz keresztül megy a k középpontján. Ha tehát a k középpontjából az e inverz köréhez érintőt szerkesztünk, ez lesz a keresett kör inverz egyenese. A megoldások száma tehát 2, 1, 0.

 

Barok György (Koháry István rg. VIII. o. Gyöngyös)

Grünwald Tibor (Eötvös József r. VIII. o. Bp.)

 

II. Megoldás. Azon körök középpontjainak mértani helye, melyek az egyenest érintik és az A ponton keresztülmennek, oly π parabola, melynek A a gyújtópontja és e az irányvonala. Azon körök középpontjainak mértani helye, melyek két kört merőlegesen metszenek*, ‐ a mi esetünkben az egyik kör az A pont, melynek sugara zérus ‐ a két kör δ hatványvonala. Eszerint meg kell keresnünk a π parabola és a δ egyenes közös pontjait. Ezen szerkesztést l. V. évf. 441. feladatban.
 

Csiky János (Dugonics András. g. VIII. o. Szeged)
 

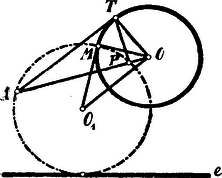
III. Megoldás. Az adott k kör középpontja legyen O, a követelménynek megfelelő k1 köré O1. A k és k1, körök egyik közös pontja legyen M, tehát OM⊥OM1. Az A pontból a k körhöz húzott érintő T érintési pontjának vetülete az AO-n legyen P.
 
 

Ekkor, az OTA derékszögű háromszögből,
OM¯2=OT¯2=OA¯⋅OP¯.

Minthogy OM a k1 kör érintője, az egyenlet azt mutatja, hogy a P pont a k1 körön fekszik. Eszerint a keresett k1 kör az adott A ponton kívül keresztülmegy még a P ponton és az e egyenest érinti. Ezen alapon a k1 kör megszerkeszthető; ilyen kör van: 2, 1, 0.
 

Grünwald Tibor (Eötvös József r. VIII. o. Bp.)
*Úgy is mondhatjuk, hogy azon pontok mértani helye amelyekre nézve az A pontról és a k kör középpontjából való távolságuk négyzetének különbsége állandó, v. ö. III. évf. 139. gyakorlat.