Kezdőlap


Feladat:	487. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. , Barok György , Dux Klára , Ernst F. , Feldheim E. , Gillemot L. , Gohn E. , Grünwald T. , Hajós György , Hapka I. , Jurenák D. , Katona Erzsébet , Klein B. , Kmoschek P. , Lázár Erzsébet , Ligeti M. , Lindtner P. , Radványi L , Sámuel J. , Scheibner Kálmán , Schossberger A. , Schwarcz F. , Sebők Gy. , Simon Á. , Sréter J. , Stern M. , Szebasztián Rózsa
Füzet:	1929/szeptember, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Pont körüli forgatás, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Egyenesek egyenlete, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1929/április: 487. matematika feladat

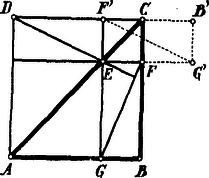
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $A B C D$ négyzetet az $A C$ átló két egyenlőszárú derékszögű háromszögre bontja. Az $A B C ▵$ -be írt változó $E G B F$ téglalap $E$ az $A C$ átlón fekszik. Írjunk az $A B C ▵$ -be is téglalapot, melynek $E$ legyen az átfogón fekvő csúcsa.

Akkor ezen téglalap

D E

átlója az előbbinek

F G

átlójára merőleges. Forgassuk ugyanis az

E G B F

téglalapot

90^{\circ}

-kal az

E

pont körül az

E G' B' F'

helyzetbe; ekkor

F' G' ⊥ F G

. Azonban

D E ⊥ F G

. Eszerint a változó

E

csúcsaiból az

F G

átlóra bocsátott merőleges mindenkor a derékszög

B

csúcsának az

A C

átfogóra nézve szimmetrikus pontján megy keresztül^{$^{*}$}

Scheibner Kálmán (gyalorló réál VI. o. Pécs.)

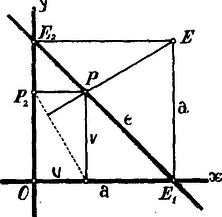
II. Megoldás. Legyen a derékszögű háromszög két befogója a derékszögű koordináta-rendszer

x

és

y

tengelyén: ha a befogó

= a

, akkor az átfogó egyenlete

\begin{matrix} x + y = a . \end{matrix}

A változó téglalapnak az átfogót befutó

P

csúcsának koordinátái legyenek

u

és

v

, akkor

\begin{matrix} u + v = a \end{matrix}

P

csúccsal szemben fekvő álló irányhatározója:

- \frac{v}{u}

; tehát a

P

pontból az átlóra bocsátott merőleges egyenes egyenlete

\begin{matrix} y - v = \frac{u}{v} (x - u) ill. y - v = \frac{u}{v} (x - u + v) \end{matrix}

Rendezve:

\begin{matrix} y = \frac{u}{v} (x - u) + (u - v), \\ y - \frac{u}{v} (x - a) + a . & (1) \end{matrix}

x = a

, akkor

y = a

u

és

v

értékeitől függetlenül, tehát az (1) egyenes mindenkor keresztül megy

x = a

y = a

ponton!

Barok György (Koháry István rg. VII. o. Gyöngyös.)

^{$^{*}$}L. még 1. évf. 4─5. számban a 26. feladatot.