| Feladat: | 480. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Barok Gy. , Cziffra A. , Erdős Pál , Fejér Gy. , Feldheim E. , Hajós György , Hapka I. , Liebermann J. , Sámuel J. , Schwarcz F. , Simon Á. | ||
| Füzet: | 1929/szeptember, 15 - 17. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Másodfokú (és arra visszavezethető) egyenletek, Negyedfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Síkgeometriai számítások trigonometria nélkül körökben, Diszkusszió, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1929/április: 480. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Megoldás. . Tegyük fel elsősorban, hogy az pont a körön belül van, azaz . A feladat egyszerűbb tárgyalása szempontjából ismeretlennek tekintsük a keresett szelőnek a kör középpontjától való távolságát. A húr felezőpontja legyen , tehát ; legyen továbbá . 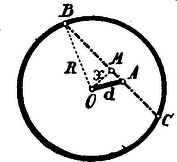 Nyilván A feladat követelménye: . Helyettesítve ezeket az előbbi összefüggések alapján: Négyzetre emelve és rendezve: Hogy a követelménynek megfeleljen, kell, hogy -nél kisebb pozitív érték legyen. A gyökök nagyobbika pozitív, de -nél nagyobb. A kisebbik gyök -nél kisebb; pozitív azonban akkor lesz, ha tekintettel arra, hogy a gyökök összege pozitív, a gyökök szorzata is pozitív, azaz Határesetben még , ha ; ekkor az ponton átmenő átmérő felel meg a követelménynek. . Tegyük fel már most, hogy az pont a körön kívül fekszik: . 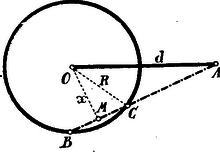 Ekkor az és értékei ugyanazok, mint . alatt, azonban Utóbbi összefüggésbe helyettesítve a
Most azonban -re nézve kell, hogy legyen: A gyökök nagyobbika pozitív, de -nél nagyobb. A kisebbik -nél kisebb. Pozitív akkor, ha Határesetben , ha ekkor is az ponton átmenő átmérő felel meg. Összefoglalva tehát kimondhatjuk, hogy a feladatnak akkor van megoldása, ha Ezen eredményt geometriailag így jellemezhetjük: húzzunk a körben az ponton keresztül átmérőt és keressük kör azon pontjait, melyek az átmérőt folytonos arányban osztják; az pontnak ezen pontok által meghatározott vonaldarabon kell feküdnie. II. Megoldás. A folytonos arányban való osztás követelményét ha , és pont a körön belül fekszik, így is felírhatjuk: Szerkesszük meg az egyenesen az pontot úgy, hogy legyen. Ekkor és így Eszerint az sugárral kört szerkesztünk az középpontból; ezen kör az adott kört két pontban metszi, úgy, hogy két szimmetrikus helyzetű (egyenlő) húrt kapunk. 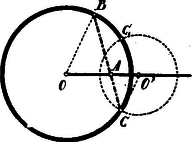 A szerkesztés lehetséges, ha a két körnek tényleg van közös pontja, azaz ha Ezen egyenlőtlenségek, a kellő rendezés után, az I. megoldásban talált . alatti Ha a folytonos arányban való osztás értelmezését kiterjesztjük arra az esetre is, amidőn az osztó pont a meghosszabbításán, tehát a körön kívül fekszik, akkor ismét Az pont most és közé esik és A szerkesztés lehetőségének feltétele: Kellő rendezés után így az I. megoldás alatti eredményéhez jutunk:
|