| Feladat: | 425. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Brünn R. , Etre S. , Fischer Gy. , Freytag A. , Gillich E. , Glosios T. , Grünwald F. , Hajós György , Klein T. , Kovács K. , Kozma F. , Pápay M. , Papp L. , Párducz N. , Sebők Gy. , Sebők I. , Soldinger J. , Szebasztián Rózsa , Szolovits D. , Turán Pál , Walient P. , Zerkovitz B. | ||
| Füzet: | 1929/január, 142. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Alakzatok hasonlósága, Körök, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1928/november: 425. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. a) Ha a kör két húrja párhuzamos és a középponttól egyenlő távolságra vannak, akkor ezen húrok oly téglalapot határoznak meg, melynek átlói a kör átmérői. 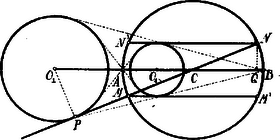 Ekkor c) A -nek egyik az -vel párhuzamos érintője messe a kört az (ill. ), a másik érintő (ill. ) pontban, úgy hogy és az a) szerint egy átmérő végpontjai. Bocsássunk az pontból az egyenesre, -ből az egyenesre merőlegest; az előbbi talppontja , az utóbbi . Az és háromszögek hasonlóságából:
Azonban , tehát (3) szerint . Másrészt és így (3) és (4) alapján . Eszerint az egyenes távolsága -től a sugarával egyenlő, amiért a érintője.
|