Kezdőlap


Feladat:	393. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Hajós György , Hapka István , Ignátz P. , Jacobi Arisztid , Klein Eszter , Pápay M. , Sréter Jenő , Turán Pál
Füzet:	1928/október, 54. oldal		PDF \| MathML
Témakör(ök):	Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1928/május: 393. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. $1^{\circ}$ . Az $A B C D$ tetraéderben legyen $D A ⊥ B C$ és $D B ⊥ C A$ , továbbá e $D$ csúcs vetülete az $A B C$ síkon az $M$ pont. Minthogy $D A ⊥ B C$ , azért $D A$ vetülete $A M ⊥ B C$ ; hasonló oknál fogva $B M ⊥ C A$ . Eszerint $M$ az $A B C ▵$ magassági pontja és így $C M ⊥ A B$ , tehát egyúttal 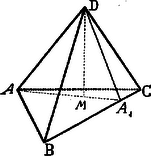$D C ⊥ A B$ .

2^{\circ}

. Az

A M

magassági vonal a

B C

oldalt

A_{1}

-ben metszi. Mivel

M A_{1}

D A_{1}

velülete és

M A_{1} ⊥ B C

, azért egyszersmind

D A_{1} ⊥ B C

. Ebből következik, hogy

\begin{matrix} {\bar{D B}}^{2} - {\bar{D C}}^{2} = {\bar{A_{1} B}}^{2} - {\bar{A_{1} C}}^{2} = {\bar{A B}}^{2} - {\bar{A C}}^{2} \end{matrix}

tehát

\begin{matrix} {\bar{D B}}^{2} + {\bar{A C}}^{2} = {\bar{D C}}^{2} + {\bar{A B}}^{2} . \end{matrix}

Ugyanígy mutathatjuk ki, hogy:

{\bar{D B}}^{2} + {\bar{A C}}^{2} = {\bar{D A}}^{2} + {\bar{B C}}^{2}

, azaz a szemben fekvö élek négyzetének összege ugyanakkora.

Jacobi Arisztid (Berzsenyi Dániel rg. VII. o. Bp. V.)

Sréter Jenő (izr. rg. VII. o. Debrecen)

II. Megoldás. Ad

2^{\circ}

. Az

A B C ▵

köré írt kör sugara legyen

R

, szögei

α

β

γ

. Ismeretes összefüggések:

\begin{matrix} B C = a = 2 R sin α; C A = b = 2 R sin β \\ a^{2} - b^{2} = 4 R^{2} (sin^{2} α - sin^{2} β) = 4 R^{2} (cos^{2} β - cos^{2} α) . \end{matrix}

Másrészt:

\begin{matrix} A M = 2 R cos α; B M = 2 R cos β \end{matrix}

tehát:

\begin{matrix} a^{2} - b^{2} = {\bar{B M}}^{2} - {\bar{A M}}^{2} azaz a^{2} + {\bar{A M}}^{2} = b^{2} + {\bar{B M}}^{2} = c^{2} + {\bar{C M}}^{2} \end{matrix}

Az utóbbi egyenlőségek mindegyik oldalához adjunk

\bar{D M^{2}}

-t; így lesz

\begin{matrix} {\bar{A M}}^{2} + {\bar{D M}}^{2} = {\bar{A D}}^{2}; {\bar{B M}}^{2} + {\bar{D M}}^{2} = {\bar{B D}}^{2}; {\bar{C M}}^{2} + {\bar{D M}}^{2} = {\bar{C D}}^{2} \end{matrix}

és

\begin{matrix} a^{2} + {\bar{A D}}^{2} = b^{2} + {\bar{B D}}^{2} = c^{2} + {\bar{C D}}^{2} . \end{matrix}

Hapka István (Dugonics András g. VI. o. Szeged)

Jegyzet. A tetraéder szemben fekvő két-két élén fektessünk párhuzamos síkokat;¹ ezáltal oly paralelepipedon keletkezik, melynek két pár szemben fekvö határlapján az átlók egymásra merőlegesek, tehát e határlapok rombuszok. Ezért a harmadik pár párhuzamos határlapon is rombuszok keletkeznek. Ebből következik úgy az

1^{\circ}

., mint a

2^{\circ}

. tétel.

Szerk.

¹L. II. évf. 161. o. és IV. évf. 346. feladatot a 215. oldalon.