|
| Feladat: |
378. matematika feladat |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Bakos T. , Hajós György , Klein Eszter , Molnár L. , Scholcz P. , Szekeres Gy. , Tóvárosi Fischer György , Turán Pál |
| Füzet: |
1928/szeptember,
18 - 21. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Parabola egyenlete, Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat |
| Hivatkozás(ok): | Feladatok: 1928/április: 378. matematika feladat |
|
|
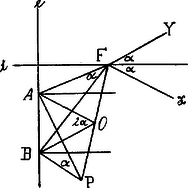
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Megoldás. Az adott szög szárai érintsék az parabolát; adva van .
A parabolának (, ), ill. (, ) pontjában húzott érintő egyenlete: ill. Tekintettel arra, hogy , és , az érintők egyenlete így is írható: ill.
Az (1a) és (2a) érintők metszéspontjának koordinátáit kell kiszámítanunk. Az (1a) és (2a) elsőfokú egyenletekből álló rendszerre nézve:
és az érintők metszéspontjának koordinátái. Az érintők hajlásszögére nézve pedig: | | (5) |
A (3), (4) és (5) egyenletekből -t és -t kiküszöbölve, és között összefüggést nyerünk; ez lesz a keresett mértani helynek egyenlete. (5)-ből A (3) és (4) alapján : .
Eszerint lesz a szög csúcsának mértani helye, ha a szög szárai a parabolát érintik. A (6) egyenletet rendezzük és | | (6a) |
alakban írva, -tel tagonként osztunk; a baloldal első két tagját teljes négyzetté egészítjük ki, miáltal az | | (7) |
egyenlethez jutunk; ebből kiolvashatjuk, hogy hiperbolával van dolgunk, melynek valós tengelye az tengely, képzetes tengelye az tengellyel párhuzamos és középpontját koordináták határozzák meg. Ha a hiperbola féltengelyei és , úgy | |
Az aszimptoták irányhatározói: .
Ha , akkor (6)-ból a mértani hely egyenlete: Ebben az esetben az adott parabolával van dolgunk, mert ebben az esetben a két érintő összeesik és a mozgó szög csúcsa a parabola illető pontja.
A hiperbola egyenlőoldalú, ha ; ezen eset nyilván akkor áll elő, ha , azaz a mozgó szög szárai -ú (-ú) szöget zárnak be. Ekkor .
Ha a mozgó szög -ú, akkor ; az (5)-ből következik, hogy most azaz a hiperbolából egyenes lesz, még pedig a parabola irányvonala.
Megjegyzendő még, hogy ha a hiperbola egyik ágán fekvő pontokból a parabolához húzott érintők szöge úgy a másik ágán fekvő pontokból a parabolához húzott érintők szöge .
| Tóvárosi Fischer György (I. é. gépészmérnök hallgató, Bp.) |
II. Megoldás. A parabola azon ismeretes tulajdonságából indulunk ki, hogy a gyújtópontjából az érintőire húzott merőlegesek talppontjainak mértani helye a parabola csúcsérintője. Legyen tehát a parabola gyújtópontja, egyenes a tengelye és a csúcsérintője. a keresett mértani hely egy pontja; ezen pontból a parabolához húzott érintők szöge tehát és ezen érintők az egyenest , ill. pontban metszik. A bevezetésben említett tulajdonságánál fogva , , , pontok az átmérőjű körön feküsznek. Ha ezen kör középpontját az és pontokkal összekötjük, és az -ban, ill. -ben az egyenesre emelt merőlegessel az állandó szöget zárja be, úgy hogy és azaz és iránya állandó.
. Forgassuk ezen szög szárait körül, az sugársor és sugársor kongruensek, tehát projektív vonatkozásban állanak egymáshoz; így az pontsor is projektív a pontsorhoz. Ha tehát az pontsorozat pontjait az egyenes végtelenben fekvő pontjával, a pontsorozat megfelelő pontjait az egyenes végtelenben fekvő pontjával kötjük össze, ismét két projektív sugársort kapunk. A megfelelő sugarak metszőpontja, eszerint kúpszeletet ír le, mely keresztűlmegy a projektív sugársorok tartóin: az és egyenesek végtelenben fekvő pontjain. E kúpszeletnek így két végtelenben fekvő pontja van, tehát hiperbola.
Ha azonban az pont hiperbolát ír le, akkor a pont evvel hasonló hiperbolát ír le, mert hiszen . E hiperbolák aszimptotái szöget zárnak be egymással.
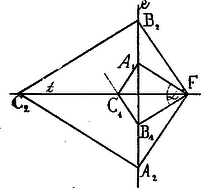
A metrikus relációk megállapítása céljából, vegyük azon két esetet, amidőn az és pontok szimmetrikus helyzetűek a egyenesre nézve; az egyik esetben , a másik esetben . A megfelelő , ill. pontok a egyenesen feküsznek, amely egyenes egyszersmind a mértani helyéül szolgáló hiperbola valós tengelye tartozik lenni, tekintettel arra, hogy a pontok erre nézve szimmetrikus helyzetűek.
Ha a parabola paramétere , akkor | |
analógiával: A hiperbola valós tengelye: | |
Minthogy az aszimptoták szöge , .
| Hajós György (kegyesrendi gimn. VII. o. Bp.) |
és ezen értékei megegyeznek az I. megoldásban nyert értékekkel! |
|
 PDF |
PDF |  MathML
MathML