Feladat: 354. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bucsy I. ,  Hajós György ,  Molnár L. ,  Pápay Miklós ,  Papp L. ,  Sveiczer Márton ,  Szekeres Gy. ,  Turán Pál ,  Wachsberger Márta 
Füzet: 1928/április, 239 - 240. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Súlypont, A háromszögek nevezetes pontjai, Négyszögek geometriája, Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):Feladatok: 1928/február: 354. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1∘. Az AC és BD, ill. AB és CD, ill. AD és BC egyenesek metszőpontjai legyenek rendre E, F, G. Az E ponton áthaladó AB-vel párhuzamos egyenes CD-t a K-ban, a BC-vel párhuzamos AD-t az L, a CD-vel párhuzamos AB-t az M, a DA-val párhuzamos BC-t az N pontban metszi. Kimutatjuk, hogy a K, L, M pontok egy egyenesen feküsznek. Ugyanis

EK∥AB≡AFésEL∥BC≡CG,tehátFKDK=BEDE=GLDL,(1)EM∥CD≡DFésEL∥CG,tehátAMFM=AECE=ALGL.(2)
(1) és (2)-ből:
FK⋅AMDK⋅FM=ALDL,azazFK⋅DL⋅AMDK⋅AL⋅FM=1.(3)

A (3) egyenlet értelmében a K, L, M pontok az ADF▵ egy szelőjén feküsznek. Ugyanígy kimutathatjuk, hogy a K, L, N pontok a CDG▵ egy szelőjén feküsznek.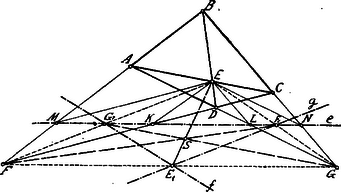
 
 

Eszerint a K, L, M, N pontok egy e egyenesen feküsznek, amely az E átlós ponthoz tartozik. Hasonlóan tartozik az F átlós ponthoz az f, a G átlós ponthoz a g egyenes.
 

2∘. Az (1)-ben láttuk, hogy FKDK=GLDL; ebből az következik, hogy KL≡e∥FG, tehát a DKL▵∼DFG▵ és hasonló helyzetűek is a D pontra nézve. Ugyanígy f∥EG és g∥EF; ezért az e, f, g egyenesek által alkotott háromszög hasonló az EFG átlós háromszöggel.
Másrészt az e egyenes felezi az EFG▵-nek EF és EG oldalait. T. i. az e egyenes LN darabja az ELGN parallelogramma átlója és így felezi az EG átlót; a KM darabja pedig, mint az EKFM parallelogramma átlója felezi a másikat, az EF-t. Hasonlóan az f egyenes felezi az EFG▵-nek FE és FG, a g egyenes pedig a GE és GF oldalait. Az e, f, g egyenesek által alkotott háromszög, csúcsai: E1, F1, G1 az EFG▵ oldalainak felezőpontjai. Ezen két háromszög hasonló helyzetű az EFG▵ súlypontjára nézve. (S).
 

Pápay Miklós (Verseghy Ferenc rg. VII. o. Szolnok)
 

II. Megoldás. Képzeljünk az E ponton át húzott tetszőleges szelőt, mely az AB és CD oldalakat α, ill. β és az FG-t ε pontban metszi. A teljes négyszögre vonatkozó alaptételek szerint ekkor (α, β) és (E, ε) harmonikus pontpárok. Ha a szelő CD-vel párhuzamos, akkor β a végtelenbe kerül és α az M pontba esik úgy, hogy felezi az Eε távolságot. Ha a szelő AB-vel párhuzamos, α a végtelenbe kerül és β a K pontba úgy, hogy K is felezi az Eε' távolságot; tehát MK∥FG és felezi EF-t, tehát EG-t is. Ugyanígy láthatjuk a BC és AD oldalakkal kapcsolatban, hogy LN∥FG és felezi EG-t, tehát EF-t is. Más szóval: az MK és LN egyenesek összeesnek és keresztülmennek az F1, G1 oldalfelező pontokon. (Analog: f∥EG és keresztülmegy az E1, G1 felező pontokon; g∥EF és keresztülmegy az E1, F1 pontokon.)
 

Hajós György (kegyesrendi gimn. VII. o. Bp.)