Kezdőlap


Feladat:	346. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bélteki J. , Blahó Magda , Bucsy I. , Erdey L. , Etre S. , Gerő L. , Gregor A. , Hajós György , Hapka I. , Klein M. , Kőrösy J. , Kozma F. , Krausz Erzsébet , Molnár L. , Papp L. , Pollák A. , Schlüssler E. , Scholcz P. , Schopp J. , Somogyi L. , Steinhauser A. , Szekeres Gy. , Szmodics Zoltán , Turán Pál , Ungár T. , Wachsberger Márta , Walient P. , Wolkóber L.
Füzet:	1928/március, 215 - 216. oldal		PDF \| MathML
Témakör(ök):	Beírt gömb, Terület, felszín, Térfogat, Szabályos tetraéder, Feladat
Hivatkozás(ok):	Feladatok: 1928/január: 346. matematika feladat

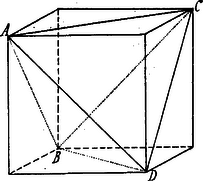
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ} .$ A szab. tetraéder két szemben fekvő élének felezőpontjait összekötő egyenes, az ún. tengely, ezen élek közös normálisa. Ha két-két szemben fekvő élen át a közös normálisukra merőleges síkot fektetünk, kockát kapunk^{$^{*}$}; a tetraéder élei a határlapok átlói. A tetraéder éleit érintőgömb nem más, mint ezen kockába írt gömb.

Ha a tetraéder éle

a

, a kockáé

d

, úgy

a = d \sqrt[]{2}

. A gömb sugara pedig

\begin{matrix} ϱ = \frac{d}{2} = \frac{a}{2 \sqrt[]{2}} = \frac{a \sqrt[]{2}}{4} . \end{matrix}

Ezen gömb középpontja felezi a kocka testátlóját; legyen ez

D

. A gömb középpontjának távolsága a tetraéder csúcsaitól:

\begin{matrix} R = \frac{D}{2} = \frac{d \sqrt[]{3}}{2} = \frac{a \sqrt[]{6}}{4} . \end{matrix}

2^{\circ} .

A gömbnek a tetraéderen kívül fekvő része gömbszelet, melyet a gömbsüveg határol.
A gömbsüveg felszíne

F = 2 ϱ π m

, ahol

m

a gömbszelet, gömbsüveg magassága; az adott esetben:

\begin{matrix} m = ϱ - \frac{R}{3} = \frac{a \sqrt[]{2}}{4} - \frac{a \sqrt[]{6}}{12} = \frac{a \sqrt[]{2}}{4} \cdot (1 - \frac{\sqrt[]{3}}{3}) \\ F = 2 ϱ π m = 2 \cdot \frac{a \sqrt[]{2}}{4} \cdot π \cdot \frac{a \sqrt[]{2}}{4} (1 - \frac{\sqrt[]{3}}{3}) = \frac{a^{2} π}{4} (1 - \frac{\sqrt[]{3}}{3}) . \end{matrix}

A gömbszelet köbtartalma:

\begin{matrix} V = \frac{m^{2} π}{3} (3 ϱ - m) = \frac{a^{2}}{3 \cdot 8} {(1 - \frac{\sqrt[]{3}}{3})}^{2} π [\frac{a \sqrt[]{2}}{2} + \frac{a \sqrt[]{6}}{12}] = \\ = \frac{a^{3} π \sqrt[]{2} \cdot 2}{3 \cdot 8 \cdot 3 \cdot 12} (2 - \sqrt[]{3}) (6 + \sqrt[]{3}) = \frac{a^{3} π \sqrt[]{2}}{432} (9 - 4 \sqrt[]{3}) . \end{matrix}

Szmodics Zoltán (Eötvös József főreál VIII. o. Bp. IV.)

^{$^{*}$}L- II. évf. 161. o.