Kezdőlap


Feladat:	332. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hajós György , Klein Eszter , Pápay Miklós , Papp L. , Szmodics Zoltán , Wolkóber L.
Füzet:	1928/február, 187 - 188. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Szögfelező egyenes, A háromszögek nevezetes pontjai, Egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1927/december: 332. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ} .$ Tegyük fel, hogy az $O$ és $O'$ pontokra nézve a kivánt összefüggés fennáll. Ekkor az $A O_{c} O O_{b}$ és $A O'_{b} O' O'_{c}$ négyszögeknek az $A$ csúcsnál közös szögük van, két-két szögük derékszög, tehát valamennyi szögük egyenlő.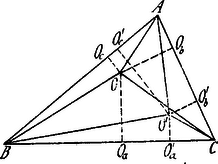

Mivel pedig feltételeztük, hogy

\begin{matrix} {\bar{O O}}_{c} \cdot {\bar{O' O'}}_{c} = {\bar{O O}}_{b} \cdot {\bar{O' O'}}_{b}, \end{matrix}

azaz

\begin{matrix} O O_{c} : O O_{b} = {\bar{O' O'}}_{b} : {\bar{O' O'}}_{c}, \end{matrix}

következik, hogy az említett két négyszög hasonló. Eszerint kell, hogy a négyszögek megfelelő átlói által létesített háromszögek is hasonlók legyenek, pl.

O A O_{c} ▵ \sim O' A O'_{b} ▵

és így

O A B ∢ = O' A C ∢

, más szóval

O A

és

O' A

szimmetrikus helyzetűek a

B A C ∢

felező egyenesére nézve.
Analóg módon következik, hogy az

O B

és

O' B

ill. az

O C

és

O' C

csúcsvonalak is szimmetrikus helyzetűek a

C B A ∢

ill.

A C B ∢

felezőjére nézve.
Szükséges tehát, hogy az

O

és

O'

pontok csúcsvonalai szimmetrikus helyzetűek legyenek az

A B C ▵

szögfelezőire nézve.

2^{\circ} .

Ezen feltétel egyszersmind elegendő. Mert, ha

O A B ∢ = O' A C ∢

továbbá

O O_{c} ⊥ A B

O' O'_{b} ⊥ A C

, akkor

A O O_{c} ▵ \sim A O' O'_{b} ▵

. De mivel

O A B ∢ = O' A C ∢

, azért

O A C ∢ = O' A B ∢

; ha már most

O O_{b} ⊥ A C

O' O'_{c} ⊥ A B

, akkor

A O O_{b} ▵ \sim A O' O'_{c} ▵

. Ennélfogva

\begin{matrix} O O_{c} : O' O'_{b} = A O : A O' = O O_{b} : O' O'_{c}, tehát {\bar{O O}}_{c} \cdot {\bar{O' O'}}_{c} = {\bar{O O}}_{b} \cdot {\bar{O' O'}}_{b} \end{matrix}

Ugyanígy bizonyítható, hogy

{\bar{O O}}_{b} \cdot {\bar{O' O'}}_{b} = {\bar{O O}}_{a} \cdot {\bar{O' O'}}_{a}

Pápay Miklós (Verseghy Ferenc rg. VII. o. Szolnok.)

II. Megoldás. Legyen a

P

pontnak az

A B C ▵

oldalaitól való távolsága rendre:

x_{a}

x_{b}

x_{c}

. Azon

P

pontok mértani helye, amelyekre nézve

\frac{x_{a}}{x_{b}} = λ = const.

oly

g

egyenes vonal, mely átmegy a

C

csúcson.
Ha a

g

egyenesnek a

C

szög felezőjére nézve szimmetrikusa

g'

, úgy ennek pontjaira nézve:

\frac{x_{a}}{x_{b}} = \frac{1}{λ}

.
Ha már most az

O

és

O'

pontokra nézve

\begin{matrix} x_{a} \cdot x'_{a} = x_{b} \cdot x'_{b} azaz \frac{x_{a}}{x_{b}} = \frac{1}{\frac{x'_{a}}{x'_{a}}}, \end{matrix}

ez azt jelenti, hogy

O C

és

O' C

egyenesek a

C

szögfelezőjére nézve szimmetrikus helyzetűek. ‐ Mutatis mutandis, áll ez a háromszög többi szögfelezőjére nézve is.
Viszont, ha

O

és

O'

oly helyzetűek hogy csúcsegyeneseik szimmetrikusak a szögfelezőre nézve, akkor fennállanak az adott relációk. Ez a feltétel tehát szükséges és elegendő.

Szmodics Zoltán (Eötvös József főreál VIII. o. Bp.)