Feladat:	321. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke Gy. ,  Böszörményi Gy. ,  Camhi S. ,  Darvas I. ,  Elek T. ,  Erdélyi L. ,  Fischer György ,  Glosios T. ,  Gregor A. ,  Hajós György ,  Jónás P. ,  Juvancz I. ,  Kárteszi Ferenc ,  Kiss F. ,  Klein M. ,  Klein T. ,  Krausz Eszter ,  Molnár L. ,  Neufeld B. ,  Papp L. ,  Petrovits G. ,  Rappaport D. ,  Schopp J. ,  Sréter J. ,  Szabó István ,  Szekeres György ,  Szivós M. ,  Szmodics Zoltán ,  Tamás Gy. ,  Turán Pál ,  Wachsberger Márta
Füzet:	1928/január, 154 - 156. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Körök, Húrnégyszögek, Négyszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1927/november: 321. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.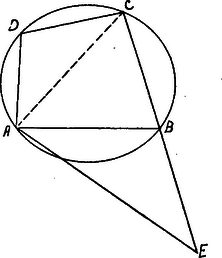   I. Megoldás. Hosszabbítsuk meg a $BC$ oldalt ‐ ábránk szerint ‐ az $E$ pontig úgy, hogy $\widehat{BAE}=\widehat{DAC}$ legyen; minthogy $\widehat{ABE}={180}^{\circ }-\widehat{ABC}=\widehat{ADC}$, következik, hogy $AB{E}_{▵}\sim AD{C}_{▵}$ tehát ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle BE:AB=CD:AD;\text{innen}BE=\frac{AB\cdot CD}{AD}\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle }& {\displaystyle EA:AB=CA:AD\text{vagy}EA:CA=AB:AD\mathrm{.}}\hfill & \text{(<mn>2</mn>)}\end{array}}$ Az (1) alapján, ha tetszőleges egyenesre felmérjük a $BC$ oldalt, megszerkeszthetjük a $BE$ távolságot, tehát a felvett egyenesen van már 3 szilárd pontunk: $B$, $C$, $E$. A (2) szerint $A$ pontnak az $E$ és $C$ szilárd pontoktól való távolságainak aránya megadott mennyiség, azaz $A$ egyrészt az Apollonius-féle körön fekszik, melyet az $E$, $C$ szilárd pontok és az $AB:AD$ arányszám határoz meg; másrészt $A$ a $B$ középpontú, $AB$ sugarú körön is fekszik, tehát $A$ ezen két kör közös pontja. Ezen két körnek két közös pontja szimmetrikus helyzetű a $BC$ egyenesre. nézve, tehát csak egy megoldása van a feladatnak. NB. Hasonlóan szerkeszthető az általános négyszög is, ha adva vannak az oldalai és két szemközt fekvő szög összege, ill. különbsége, de ekkor az $E$ pont nem fekszik a $BC$-n és így általában két különböző négyszöget kapunk.   Szmodics Zoltán (Eötvös József főreál VIII. o. Bp. IV.)   II. Megoldás. Szerkesszünk az $ABCD$ húrnégyszöghöz hasonló négyszöget a $CA\text{'}D\text{'}B$ négyszöget úgy, hogy $A\text{'}$ a $DC$ és $D\text{'}$ az $AB$ meghosszabbításán feküdjék és megfelelő csúcspárok: 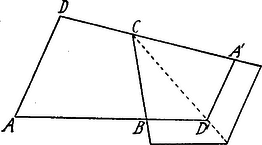$\begin{array}{c}{\displaystyle A-C\mathrm{,}B-A\text{'}\mathrm{,}C-D\text{'}\mathrm{,}D-B\mathrm{.}}\end{array}$   A húrnégyszög szögeinek tulajdonságaiból következik, hogy $A\text{'}D\text{'}||AD$. Másrészt; ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle CA\text{'}:AB}& {\displaystyle =CB:AD\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle A\text{'}D\text{'}:CB}& {\displaystyle =CB:AD\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle BD\text{'}:CD}& {\displaystyle =CB:AD\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Az (1), (2), (3) egyenletekből a $CA\text{'}$, $A\text{'}D$, $BD\text{'}$ kiszámíthatók és szerkeszthetők, és így az $ADA\text{'}D\text{'}$ trapéz minden oldala ismeretes lesz. Megszerkesztve most már az $ADA\text{'}D\text{'}$ trapézt, megkaphatjuk az $ABCD$ négyszöget is.   Kárteszi Ferenc (bölcsészethallgató Bp.)   III. Megoldás. Legyen $AB=a$, $BC=b$, $CD=c$, $DA=d$ és pl. $a>c$. Hosszabbítsuk meg a $BC$ és $AD$ oldalakat, amíg $O$ pontban metszik egymást. $OD=x$, $OC=y$. Minthogy $ODC▵\sim OBA▵$, $\begin{array}{c}{\displaystyle x:c=\left(y+b\right):a}\end{array}$ (1) és $\begin{array}{c}{\displaystyle y:c=\left(x+d\right):a\mathrm{.}}\end{array}$ (2) Ezen két egyenletből;