Kezdőlap


Feladat:	308. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bucsy I. , Camhi Sámuel , Erdélyi L. , Gerő L. , Hajós György , Jónás P. , Klein Eszter , Klein M. , Klein Tibor , Molnár L. , Petrovits G. , Pollák A. , Rosenthal E. , Sréter J. , Szolovits D. , Turán Pál , Ulmer R. , Wachsberger Márta
Füzet:	1927/december, 120 - 121. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Mértani helyek, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1927/október: 308. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A két kör középpontja legyen $O_{1}$ és $O_{2}$ . A $C$ pontot vegyük fel pl. az $O_{2}$ körön. Az $A$ , ill. $B$ pontban húzzunk érintőket $O_{1}$ körhöz, amelyek az $O_{2}$ kört $A'$ , ill. $B'$ pontban metszik.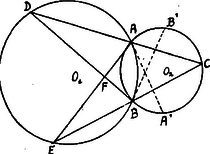
$α)$ Legyen a $C$ pont az $O_{2}$ körnek azon $A' B'$ ívén, amelyen nem feküsznek az $A$ és $B$ pontok. Az $A E$ és $B D$ egyenesek metszőpontja legyen $F$ .

A F B ∢

A D F ▵

külső szöge, tehát

A F B ∢ = F A D ∢ + A D F ∢

. Hasonlóan

F A D ∢ = A E C ∢ + A C E ∢

. Tehát

A F B ∢ = A E C ∢ + A C E ∢ + A D F ∢ = 2 A E C ∢ + A C E ∢

mivel t. i.

A E C ∢ \equiv A E B ∢

és

A D F ∢ \equiv A D B ∢

és így

A E C ∢

ugyanazon

A B

íven fekvő kerületi szög, mint az

A D F ∢

(az

O_{1}

körben), tehát

A E C ∢ = A D F ∢

. Eszerint az

A F B ∢

állandó nagyságú;

A E C ∢

O_{1}

kör,

A C E ∢

pedig az

O_{2}

kör

A B

ívéhez tartozó kerületi szögek.

F

pont mértani helye körív, mely az

A

B

pontokon megy keresztül. Ha a változó

C

pont az

A'

, ill.

B'

pontba jut,

F

pont az

A

, ill.

B

pontba esik.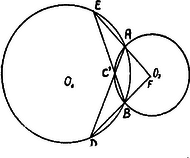

β)

C

O_{2}

körnek azon

A' B'

ívén van, pl. a

C'

helyzetben, amelyen

A

és

B

feküsznek, akkor az

A F D ▵

-ben

A F D ∢ \equiv A F B ∢

és így

\begin{matrix} 180^{\circ} - A F B ∢ = F A D ∢ + A D F ∢ . \end{matrix}

F A D ∢

A C' E ▵

külső szöge:

\begin{matrix} F A D ∢ = A E C' ∢ + E C' A ∢ . \end{matrix}

Azonban

A E C' ∢ \equiv A E B ∢

O_{1}

körben az

A B

ívhez tartozó kerületi szög; ugyanezen íven áll az

\begin{matrix} A D B' ∢ \equiv A D F ∢ is, tehát A E C' ∢ = A D F ∢ . \end{matrix}

Tekintettel ezekre,

\begin{matrix} 180^{\circ} - A F B ∢ = A E C' ∢ + E C' A ∢ + A D F ∢ = 2 A E C' ∢ + E C' A ∢ . \end{matrix}

Azonban

E C' A ∢ = 180^{\circ} - A C' B ∢ = A C B ∢

(az

α)

alatti) és így

\begin{matrix} 180^{\circ} - A F B ∢ = 2 A E B' ∢ + A C B ∢ \\ A F B ∢ = 180^{\circ} - (2 A E B' ∢ + A C B ∢) \end{matrix}

azaz most az

A F B ∢

α)

alatti kiegészítő szöge; tehát

F

pont mértani helye most ugyanazon kör másik íve.

Camhi Sámuel (izr. rg. VII. o. Bp.)