Kezdőlap


Feladat:	306. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Böszörményi Gy. , Camhi S. , Glosios T. , Hajós György , Klein Eszter , Klein M. , Klein T. , Molnár L. , Neufeld B. , Rappaport D. , Turán Pál , Wachsberger Márta , Wolkóber L.
Füzet:	1927/december, 118 - 120. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Szögfelező egyenes, Beírt kör, Kör (és részhalmaza), mint mértani hely, Háromszögek szerkesztése, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1927/október: 306. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $A D$ szögfelező a $B C$ oldalt úgy osztja $B D$ és $C D$ részekre, hogy $A B : A C = B D : C D$ , vagyis

\begin{matrix} \frac{A B}{B D} = \frac{A C}{C D} = \frac{A B + A C}{B D + C D} = \frac{b + c}{a} . \end{matrix}

Ezen megállapítást most már úgy értelmezhetjük, hogy a

B

és

C

csúcsok mértani helye azon kör, melynek pontjaira nézve a szilárd

A

és

D

pontoktól való távolságok aránya állandó és adataink szerint ismeretes. Ezt a kört tehát, ha az

A D = d

szögfelezőt egy egyenesre lemértük megszerkeszthetjük.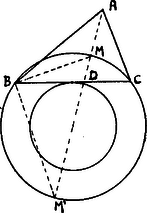

Megkeressük az

M

és

M'

pontokat az

A D

egyenesén úgy, hogy

\frac{A M}{M D} = - \frac{A M'}{M' D} = \frac{b + c}{a}

legyen (tehát

(A, D)

és

(M, M'

) harmonikus pontpárok).

M M'

lesz a kör átmérője.
Hogy ezen körnek

B

és

C

pontjait megkapjuk a

D

ponton át megadott hosszúságú

(B C = a)

húrt kell fektetnünk. Helyezzük el tehát az

a

hosszúságú húrt tetszőlegesen a körben és rajzoljunk evvel koncentrikus kört, mely az

a

hosszúságú húrt érinti. Ezen utóbbi körhöz a

D

pontból érintőt húzva, ezen érintőnek az előbbi körben fekvő darabja lesz a háromszög

B C = a

oldala.

D

pontból két érintőt húzhatunk a belső körhöz; azonban az így keletkező két háromszög egybevágó.
Vizsgáljuk meg a szerkesztés lehetőségének feltételét. Ezen feltétel nyilván nem más, mint hogy az

M M'

átmérőjű körben lehessen az

a

hosszúságú húrt elhelyezni, azaz kell, hogy

M M' \geq a

legyen. Az előbbiek alapján

\begin{matrix} (A M + M D) : M D = (b + c + a) : a, tehát M D = \frac{\bar{A D} \cdot a}{b + c + a} = \frac{d a}{b + c + a} \\ (A M' - D M') : D M' = (b + c - a) : a, tehát D M' = \frac{\bar{A D} \cdot a}{b + c - a} = \frac{d a}{b + c - a} \\ M M' = M D + D M' = \frac{d a}{b + c + a} + \frac{d a}{b + c - a} \geq a . \end{matrix}

Ezen relációból

d

-re nézve a következő megszorítás áll elő:

\begin{matrix} d \geq \frac{{(b + c)}^{2} - a^{2}}{2 (b + c)} . \end{matrix}

Ha azonban

a

-t és

d

-t választottuk szabadon, akkor

\begin{matrix} a < b + c \leq \sqrt[]{a^{2} - d^{2}} + d \end{matrix}

lesz a szerkesztés lehetőségének feltétele.

Szerk.

II. Megoldás. Az előbbi megoldásban láttuk, hogy

\begin{matrix} A B : B D = (b + c) : a . \end{matrix}

Ha az

M

pontra nézve

\begin{matrix} A M : M D = (b + c) : a, \end{matrix}

akkor

\begin{matrix} A M : M D = A B : B D, \end{matrix}

tehát

B M

\hat{A B C}

felezője tartozik lenni és így

M

A B C ▵

-be írt kör középpontja. (

M'

A B C ▵

-höz írt kör középpontja.)
Szerkesszünk

A M

mint átmérő fölött kört; ezen körben az

A

pontból kiinduló

\frac{b + c - a}{2}

hosszúságú húrok végpontjai az

A B C ▵

-be írt körnek az

A B

, ill.

A C

oldalakkal való érintési pontjai lesznek. Ilyen módon megszerkeszthetjük az

A B C ▵

-be írt kört is. Ha az előbb nevezett húrokat meghosszabbítjuk és

D

pontból a beírt körhöz érintőt húzunk, megkapjuk az

A B C ▵

-et. A két érintő két egybevágó háromszöget hoz létre.

Wachsberger Márta (izr. leánygimn. VIII. o. Bp.)

Klein Eszter (izr. leánygimn. VIII. o. Bp.)

Jegyzet. A II. megoldás lehetőségének feltétele, hogy

\begin{matrix} \frac{b + c - a}{2} \leq A M \end{matrix}

tehát

\frac{b + c - a}{2} \leq \frac{d (b + c)}{b + c + a}

. Ez megegyezik az I. megoldásban levezetett feltétellel.