Kezdőlap


Feladat:	286. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Tibor , Beke Gyula , Elek T. , Hajós György , Katona E. , Molnár László , Ság M. , Tóvárosi Fischer György , Turán Pál , Wachsberger Márta
Füzet:	1927/december, 123 - 125. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Hozzáírt körök, Ellipszis egyenlete, Ellipszis, mint mértani hely, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1927/május: 286. matematika feladat

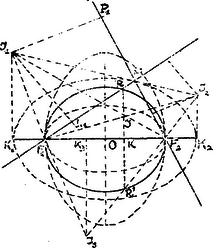
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen az ellipszis nagytengelye $2 a$ , a fókusztávolság: $F_{1} F_{2} = 2 c$ az $F_{1} F_{2} M ▵$ -be írt kör középpontja $I$ , a hozzáírt köröké az ábra szerint: $I_{1}$ , $I_{2}$ , $I_{3}$ . Továbbá $K_{1}$ , $L_{1}$ , $P_{1}$ , az $I_{1}$ , kör, $K_{2}$ , $L_{2}$ , $P_{2}$ az $I_{2}$ kör érintési pontjai.

Minthogy

\begin{matrix} F_{1} L_{1} = F_{1} K_{1}, azért F_{1} M = F_{1} L_{1} + L_{1} M = F_{1} K_{1} + L_{1} M . \end{matrix}

Minthogy

\begin{matrix} F_{2} P_{1} = F_{1} K_{1}, azért F_{2} M = F_{2} P_{1} - P_{1} M = F_{2} K_{1} - P_{1} M . \end{matrix}

Tekintettel arra, hogy

L_{1} M = P_{1} M

és

M

az ellipszis valamely pontja,

\begin{matrix} F_{1} M + F_{2} M = F_{1} K_{1} + F_{2} K_{1} = 2 a, \end{matrix}

azaz

K_{1}

szintén pontja az ellipszisnek, más szóval: az

I_{1}

pont vetülete a nagy tengelyen mindenkor az ellipszisnek a nagy tengelyen fekvő

K_{1}

pontja, tehát

I_{1}

mértani helye a

K_{1}

pontban, az ellipszis nagytengelyére emelt merőleges egyenes. Ugyanígy az

I_{2}

mértani helye a

K_{2}

pontban a nagy tengelyre emelt merőleges egyenes.
Keressük már most az

I

pont mértani helyét. Ha a beírt kör az

F_{1} F_{2}

-t

K

pontban érinti,

\begin{matrix} F_{1} I K ▵ \sim F_{1} I_{1} K_{1} ▵, tehát \frac{I K}{F_{1} K} = \frac{K_{1} F_{1}}{K_{1} I_{1}}; \end{matrix}