Kezdőlap


Feladat:	238. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Beke Béla , Beke Gy. , Elek T. , Fischer Gy. , Fürst L. , Hajós Gy. , Hallóssy Zoltán , Kozma A. , Lukács Ernő , Rochlitz K. , Ság M. , Sréter J. , Szántó L. , Tóth A. , Turán P. , Wachsberger Márta
Füzet:	1927/április, 243 - 244. oldal		PDF \| MathML
Témakör(ök):	Négyzetszámok összege, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1927/január: 238. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A tetraéder csúcsai legyenek $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4},$ a súlyvonalai $s_{1}$ , $s_{2}$ , $s_{3}$ , $s_{4} .$ Az $A_{1}$ csúcsból kiinduló $s_{1}$ súlyvonal az $A_{2} A_{3} A_{4} ▵$ súlypontján, $S_{1}$ -n megy keresztül.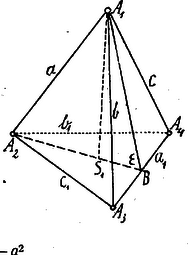

A_{2} S_{1}

A_{2} A_{3} A_{4} ▵

egyik súlyvonala; az

A_{3} A_{4}

élet felezi

B

pontban.

A_{1} B

pedig az

A_{1} A_{3} A_{4} ▵

egyik súlyvonala. Ha már most

A_{2} B = t_{2},

A_{1} B = t_{1}

és

A_{2} B A_{1} ∢ = ϵ,

akkor

\begin{matrix} \bar{A_{1} S_{1}^{2}} = s_{1}^{2} = \frac{t_{2}^{2}}{9} + t_{1}^{2} - 2 t_{1} \frac{t_{2}}{3} cos ϵ . \end{matrix}

(1)

cos ϵ

kifejezhető az

A_{1} A_{2} B ▵

-ből: ha

A_{1} A_{2} = a

, akkor

\begin{matrix} cos ϵ = \frac{t_{1}^{2} + t_{2}^{2} - a^{2}}{2 t_{1} t_{2}} . \end{matrix}

Ha ezt (1)-be helyettesítjük,

\begin{matrix} 9 s_{1}^{2} = 3 a^{2} - 2 t_{2}^{2} + 6 t_{1}^{2} . \end{matrix}

(2)

Legyen

A_{1} A_{3} = b,

A_{1} A_{4} = c;

A_{3} A_{4} = a_{1},

A_{2} A_{4} = b_{1},

A_{2} A_{3} = c_{1} .

t_{2},

mint az

A_{2} A_{3} A_{4} ▵

súlyvonala, és

t_{1}

, mint az

A_{1} A_{3} A_{4} ▵

súlyvonala kifejezhető az ismert módon:

\begin{matrix} t_{2}^{2} = \frac{2 (b_{1}^{2} + c_{1}^{2}) - a_{1}^{2}}{4}; t_{1}^{2} = \frac{2 (b^{2} + c^{2}) - a_{1}^{2}}{4} . \end{matrix}

Ha ezeket (2)-be helyettesítjük

\begin{matrix} 9 s_{1}^{2} = 3 (a^{2} + b^{2} + c^{2}) - (a_{1}^{2} + b_{1}^{2} + c_{1}^{2}) . \end{matrix}

Analog:

\begin{matrix} 9 s_{2}^{2} = 3 (a^{2} + b_{1} + c_{1}^{2}) - (a_{1}^{2} + b^{2} + c^{2}) \\ 9 s_{3}^{2} = 3 (a_{1}^{2} + b^{2} + c_{1}^{2}) - (a^{2} + b_{1}^{2} + c^{2}) \\ 9 s_{4}^{2} = 3 (a_{1}^{2} + b_{1}^{2} + c^{2}) - (a^{2} + b^{2} + c_{1}^{2}) . \end{matrix}

Összeadva:

\begin{matrix} 9 (s_{1}^{2} + s_{2}^{2} + s_{3}^{2} + s_{4}^{2}) = 4 (a^{2} + b^{2} + c^{2} + a_{1}^{2} + b_{1}^{2} + c_{1}^{2}) . \\ (s_{1}^{2} + s_{2}^{2} + c_{3}^{2} + s_{4}^{2}) : (a^{2} + b^{2} + c^{2} + a_{1}^{2} + b_{1}^{2} + c_{1}^{2}) = 4 : 9. \end{matrix}

Beke Béla (Toldi Ferenc főreál VII. o. Bp.)

II. Megoldás. A tetraéder csúcsainak koordinátái legyenek:

\begin{matrix} x_{i}, y_{i}, z_{i} (i = 1, 2, 3, 4) . \end{matrix}

A_{2} A_{3} A_{4}

határlap súlypontjának koordinátái

\begin{matrix} x' = \frac{x_{2} + x_{3} + x_{4}}{3}, y' = \frac{y_{2} + y_{3} + y_{4}}{3}, z' = \frac{z_{2} + z_{3} + z_{4}}{3} . \end{matrix}

Eszerint az

A_{1} S_{1}

súlyvonal négyzete

\begin{matrix} \bar{A_{1} S_{1}^{2}} = s_{1}^{2} = {(x - x')}^{2} + {(y - y')}^{2} + {(z - z')}^{2} = \\ = \frac{9 x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{4}^{2} - 6 x_{1} (x_{2} + x_{3} + x_{4}) + 2 (x_{2} x_{3} + x_{2} x_{4} + x_{3} x_{3})}{9} + \\ + f (y_{1}, y_{2}, y_{3}, y_{4}) + f (z_{1}, z_{2}, z_{3}, z_{4}), \end{matrix}

ahol

f

ugyanolyan szerkezetű kifejezést jelöl az

y

ill.

z

értékekből, mint amilyen az első tag.
Ha már most

s_{2}^{2}

s_{3}^{2}

s_{4}^{2}

értékét képezzük, akkor

\begin{matrix} s_{1}^{2} + s_{2}^{2} + s_{3}^{2} + s_{4}^{2} = \frac{12 {\sum_{i = 1}^{4}}_{}^{} x_{i}^{2} - 8 {\sum_{i, k = 1 (i \mp k)}^{4}}_{}^{} x_{i} x_{k}}{9} + φ (y_{1}, y_{2}, y_{3}, y_{4}) + φ (z_{1}, z_{2}, z_{3}, z_{4}) \end{matrix}

φ

az első taghoz hasonló szerkezetű kifejezést jelöl: Másrészt az

A_{i} A_{k}

él négyzete:

\begin{matrix} {\bar{A_{i} A}}_{k}^{2} = {(x_{i} - x_{k})}^{2} + {(y_{i} - y_{k})}^{2} + {(z_{i} - z_{k})}^{2} \\ {\sum_{\binom{i, k = 1}{i + k}}^{4}}_{}^{} {\bar{A_{i} A}}_{k}^{2} = 3 \sum_{i = 1}^{4} & x_{1}^{2} - 2 {\sum_{\binom{i, k = 1}{i \mp 1}}^{4}}_{}^{} x_{i} x_{k} + 3 \sum_{i = 1}^{4} y_{i}^{2} - 2 {\sum_{\binom{i, k = 1}{i \mp k}}^{4}}_{}^{} y_{i} y_{k} + 3 \sum_{i = 1}^{4} z_{i}^{2} - 2 {\sum_{\binom{i, k = 1}{i \mp k}}^{4}}_{}^{} z_{i} z_{k} \\ \frac{4}{9} \sum {\bar{A_{i} A}}_{k}^{2} = s_{1}^{2} + s_{2}^{2} + s_{3}^{2} + s_{4}^{2} . \end{matrix}

Lukács Ernő (kegyesrendi gimn. VIII. o. Bp.)

Hallóssy Zoltán (ciszterci rg. VIII. o. Bp.)