Kezdőlap


Feladat:	224. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Beke B. , Beke Gy. , Bleier P. , Elek T. , Fischer Gy. , Fürst L. , Geiringer F. , Hajdu Gy. , Hajós Gy. , Katona E. , Klein Eszter , Kornhauser József , Lukács E. , Németh B. , Ság M. , Wachsberger Márta
Füzet:	1927/február, 188 - 189. oldal		PDF \| MathML
Témakör(ök):	Trigonometria, Térelemek és részeik, Térgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1926/december: 224. matematika feladat

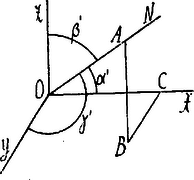
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Ha a tér tetszőleges $O$ pontjából a három adott egyenessel párhuzamost húzunk, oly háromélű testszögletet kapunk, melynek mindegyik oldala derékszögű; legyenek az élek $O x$ , $O y$ , $O z$ . Állítsunk $O$ pontból az adott $S$ síkra merőleges egyenest, $O N$ -t és ezen vegyük fel tetszőlegesen az $A$ pontot. $A$ pont merőleges vetülete az $x y$ síkon legyen $B$ és $B C ⊥ O x$ .

Ekkor

O A

felfogható, mint egy derékszögű paralelepipedon átlója, melynek élei

O C

B C

A B

, tehát

\begin{matrix} {\bar{O C}}^{2} + {\bar{B C}}^{2} + {\bar{A B}}^{2} = {\bar{O A}}^{2} \end{matrix}

vagy

\begin{matrix} {(\frac{O C}{O A})}^{2} + {(\frac{B C}{O A})}^{2} + {(\frac{A B}{O A})}^{2} = 1. \end{matrix}

(1)

O N

O x

O y

O z

egyenesekkel

α'

β'

γ'

szögeket zárja be, akkor

\begin{matrix} \frac{O C}{O A} = cos α', \frac{B C}{O A} = cos β', \frac{A B}{O A} = cos γ', \end{matrix}

tehát (1) szerint:

\begin{matrix} cos^{2} α' + cos^{2} β' + cos^{2} γ' = 1. \end{matrix}

(2)

O x

O y

O z

egyenesek az

S

síkhoz rendre

α

β

γ

szögek alatt hajlanak és mivel

O N ⊥ S

\begin{matrix} α' = 90^{\circ} - α, β' = 90^{\circ} - β, γ' = 90^{\circ} - γ \end{matrix}

és így

\begin{matrix} cos α' = sin α, cos β' = sin β, cos γ' = sin γ, \end{matrix}

tehát (2)-be helyettesítve:

\begin{matrix} sin^{2} α + sin^{2} β + sin^{2} γ = 1 \end{matrix}

vagyis:

\begin{matrix} 1 - cos^{2} α + 1 - cos^{2} β + 1 - cos^{2} γ = 1 \end{matrix}

és ebből

\begin{matrix} cos^{2} α + cos^{2} β + cos^{2} γ = 2. \end{matrix}

Kornhauser József (áll. főreál VIII. o. Eger)

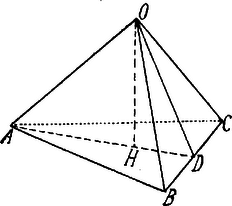
II. Megoldás. Húzzunk ismét

O

pontból a 3 adott egyenessel párhuzamosakat és az így keletkező háromélű testszöglet éleit az adott

S

sík messe

A

B

C

pontokban.

Legyen

O

pont vetülete az

A B C \equiv S

síkon

H

; ki kell mutatnunk, hogy ‐ mivel

O A H ∢ = α

O B H ∢ = β

O C H ∢ = γ

‐

\begin{matrix} \frac{{\bar{A H}}^{2}}{{\bar{A O}}^{2}} + \frac{{\bar{B H}}^{2}}{{\bar{B O}}^{2}} + \frac{{\bar{C H}}^{2}}{{\bar{C O}}^{2}} = 2 \end{matrix}

vagy, mivel

\begin{matrix} {\bar{A H}}^{2} = {\bar{A O}}^{2} - {\bar{O H}}^{2}; \end{matrix}