Kezdőlap


Feladat:	219. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Beke Gy. , Böszörményi Gy. , Elek T. , Fischer Gy. , Fürst L. , Geiringer F. , Hajós Gy. , Hallóssy Zoltán , Katona E. , Klein Eszter , Lukács E. , Mérei I. , Rochlitz K. , Ság M. , Szántó L. , Turán Pál , Wachsberger Márta , Weisz S.
Füzet:	1927/február, 181 - 183. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Függvényvizsgálat, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1926/december: 219. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $A$ csúcsból a $B C$ oldalra bocsátott merőleges legyen az $x$ -tengely és ennek poz. iránya a $B C$ felé essék. A csúcs távolsága $B C$ -től legyen $m$ . Ha a $P$ pont a $B C$ -n innen van, akkor, mivel $P D C ▵ \sim P A R ▵$ ,

\begin{matrix} A P : P D = A R : D C \end{matrix}

Innen

\begin{matrix} y = \frac{a x}{2 (m - x)} és a P Q R ▵ területe t = x y = \frac{a x^{2}}{2 (m - x)} . \end{matrix}

(1)

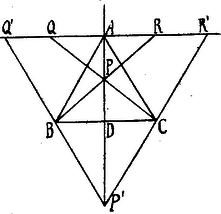Ha azonban

\begin{matrix} A P' = x > m, akkor x : (x - m) = y : \frac{a}{2} \end{matrix}

és így

\begin{matrix} y = \frac{a x}{2 (x - m)}; \end{matrix}

(2)

A területnek (1) alatti értéke érvényes akkor is, ha

x

negatív, azaz

P

-t az

A

elválasztja a

B C

-től. Az (1) alatti értékből kiolvashatjuk, hogy ha

x

változik

- \infty

-től 0-ig,

t

értéke

+ \infty

-től fogy 0-ig, mert a számláló folyton csökken, a nevező pedig növekedik. Ha pedig

x

most már 0-tól változik

m

-ig,

t

értéke növekedik 0-tól

+ \infty

-ig; ekkor ugyanis a számláló növekedik az

a m^{2}

véges értékig, a nevező pedig csökken 0-ig. Tehát, ha a

P

pont

A

-ban van

t

értéke minimum.
Ha már most

x > m

, a (2) érték azt mutatja, hogy

t

értéke

x = m

esetében

+ \infty

és

x = + \infty

esetében szintén

+ \infty

. Minthogy

t

értékét jelző függvény

x = m

helytől

x = + \infty

-ig folytonos, közben kell lennie legalább egy minimumnak. Vizsgáljuk meg tehát

t

-nek

x

szerinti első és második differenciálhányadosát.

\begin{matrix} t' = \frac{a}{2} \cdot \frac{2 x (x - m) - x^{2}}{{(x - m)}^{2}} = \frac{a}{2} \cdot \frac{x^{2} - 2 m x}{{(x - m)}^{2}} . \\ t' = 0 ha x^{2} - 2 m x = 0, tehát ha x_{1} = 0 és x_{2} = 2 m . \end{matrix}

x_{1} = 0

nem esik a most vizsgált tartományba. Csak

x_{2} = 2 m

felelhet meg.

\begin{matrix} t'' = \frac{a}{2} \cdot \frac{(2 x - 2 m) {(x - m)}^{2} - (x^{2} - 2 m x) \cdot 2 \cdot (x - m)}{{(x - m)}^{4}} = \frac{a}{2} \cdot \frac{2 {(x - m)}^{3} - 2 x (x - m) (x - 2 m)}{{(x - m)}^{4}} \end{matrix}

Helyettesítsünk

x

helyébe

2 m

-t; akkor

\begin{matrix} t'' = \frac{a}{2} \cdot \frac{2 m^{3}}{m^{4}} = \frac{a}{m} > 0 \end{matrix}

tehát

x = 2 m

helyen

t

-nek minimuma van.

Hallóssy Zoltán (ciszterci rg. VIII. o. Bp.)

II. Megoldás. A vizsgált terület szélső értékének meghatározására a

t = \frac{a x^{2}}{2 (x - m)}

egyenletet hozzuk a következő alakra:

\begin{matrix} a x^{2} - 2 t x + 2 t m = 0. \end{matrix}

(1)

Ezen egyenletnek valós gyökei csak akkor vannak, ha

\begin{matrix} 4 t^{2} - 8 t m a = 4 t (t - 2 m a) \geq 0, \end{matrix}

azaz,

t = 0

esetet kizárva,

t \geq 2 a m

.
Ebből látjuk, hogy a területnek minimuma:

2 a m

, az

A B C ▵

területének négyszerese. Ha ezen értéket az (1)-be helyettesítjük:

\begin{matrix} a (x^{2} - 4 m x + 4 m^{2}) = a {(x - 2 m)}^{2} = 0 azaz x = 2 m . \end{matrix}

Turán Pál (Madách Imre fg. VII. o. Bp.)