Kezdőlap


Feladat:	203. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beke B. , Bleier P. , Böszörményi Gy. , Csalán E. , Elek T. , Emhő L. , Erdélyi I. , Erdős P. , Fischer Gy. , Fürst L. , Glatz L. , Hajós Gy. , Hollóssy Zoltán , Katona E. , Klein Eszter , Kőrösy J. , Lukács E. , Löbl E. , Márkus L. , Máté J. , Mérei I. , Mischung Ilona , Molnár L. , Németh B. , Rosenheim L. , Rosenthal E. , Róth I. , Ság M. , Saile P. , Sréter J. , Steiner S. , Sveiczer M. , Szántó L. , Székely Lilly , Szentkirályi E. , Turán P. , Wachsberger Márta
Füzet:	1927/január, 139 - 140. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Gördülés (Mozgási geometria), Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1926/november: 203. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Induljunk ki abból a helyzetből, amidőn a gördülő kör $A$ pontja a nagyobbik körön van; a gördülő kör tetszőleges helyzetében ezután a középpontja $C$ -ben van és az $A$ kerületi pontja $M$ -be kerül, és ekkor $B$ kerületi pont van a nagy körön. Ekkor tehát a $B A$ és $B M$ ívek egyenlők; a hozzájuk tartozó középponti szögek pedig a sugarakkal fordítva arányosak, tehát 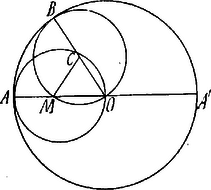$B C M ∢ = 2 B O A ∢$ .

Kössük össze

O

-t

M

-mel. A

B C M ∢

C O M

egyenlőszárú háromszög külső szöge és így

\begin{matrix} B C M ∢ = 2 B O M ∢, tehát B O M ∢ = B O A ∢, \end{matrix}

azaz

M

pont az

O A

egyenesen fekszik. Eszerint a gördülő kör

A

kerületi pontja leírja az

A A'

átmérőt, még pedig oda és vissza, mialatt az

A

pont eredeti helyzetébe kerül.

Mischung Ilona (szegedi leánygimn. VIII. o.)

II. Megoldás. A

C A

sugarú kör az

O A

sugarú kör belsejében gördül. Amikor

C

középpont

C_{1}

-ben van,

A

pont kerül

A_{1}

-be és így

\hat{A B} = \hat{A_{1} B}

hosszúságra nézve. Legyen

A O B ∢ = α

és

A_{1} C_{1} B ∢ = ε

. Akkor az egyenlő hosszúságú íveknek megfelelő szögek a két körben a sugarakkal fordítva arányosak: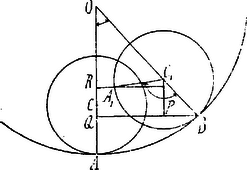

\begin{matrix} ε : α = \bar{O A} : \bar{C A} . \end{matrix}

A_{1}

pont távolsága az

O A

egyenestől

x = R A_{1}

. Minthogy

\bar{B Q} = \bar{O B} \cdot sin α

, és a

B O P ▵

-ben

\bar{B P} = \bar{C_{1} B} \cdot sin α

, továbbá

A_{1}

pont távolsága

\bar{C_{1} P}

-től

\bar{C_{1} A_{1}} sin (ε - α)

, azért

\begin{matrix} x = \bar{O B} sin α - \bar{C_{1} B} sin α - \bar{C_{1} A_{1}} sin (ε - α) . \end{matrix}

Az adott esetben:

\bar{O B} = 2 \bar{C_{1} B} = 2 \bar{C_{1} A_{1}}

és ezért

ε = 2 α

\begin{matrix} x = 2 \bar{C_{1} B} sin α - \bar{C_{1} B} sin α - \bar{C_{1} B} sin (2 α - α) = 0. \end{matrix}

Ez tehát annyit jelent, hogy

A_{1}

pont az

O A

egyenesen fekszik.

Hallóssy Zoltán (ciszterci rg. VIII. o. Bp.)