Kezdőlap


Feladat:	197. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Beke B. , Beke Gy. , Bleier P. , Böszörményi Gy. , Csalán E. , Elek T. , Fischer Gy. , Fischer Rózsi , Gregor A. , Hajós Gy. , Hallóssy Z. , Kovács J. , Lukács E. , Németh Bernáth , Neufeld B. , Ság M. , Saile P. , Sréter J. , Sveiczer M. , Szántó L. , Szentkirályi E. , Szolovits D. , Turán P. , Wachsberger Márta
Füzet:	1926/december, 117 - 118. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Beírt alakzatok, Geometriai egyenlőtlenségek, Terület, felszín, Négyszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1926/október: 197. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Szerkesszünk az $A B$ oldal fölött négyzetet; ennek $D$ és $E$ csúcsait kössük össze a háromszög $C$ csúcsával. Ezen összekötő egyenesek az $A B$ oldalon meghatározzák a négyzet $K L$ alapját. Állítsunk $K$ és $L$ pontokban az $A B$ -re merőlegeseket, megkapjuk az $A C$ , ill. $B C$ oldalon a négyzet $N$ , ill. $M$ csúcs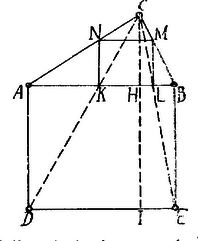át.

Ugyanis:

\begin{matrix} C K L ▵ \sim C D E ▵, tehát K L : D E = C K : C D = C L : C E, & (1) \\ C K N ▵ \sim C D A ▵,, K N : A D = C K : C D, & (2) \\ C L M ▵ \sim C E B ▵,, L M : B E = C L : C E . & (3) \end{matrix}

Minthogy

A D = D E

, azért (1) és (2) alapján

K N = K L

.
Mivel

B E = D E

, azért (1) és (3) alapján

L M = K L

.
Eszerint a

K L M N

idom csakugyan négyzet.

2^{\circ}

. A három négyzet közül annak van legnagyobb területe, melynek oldala a legnagyobb. Legyen

D E = A B = c

\begin{matrix} K L : D E = C H : C I \end{matrix}