Kezdőlap


Feladat:	196. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Beke B. , Beke Gy. , Bleier P. , Fischer Gy. , Fischer Rózsi , Hajós Gy. , Hallóssy Z. , Kozma A. , Németh B. , Ság M. , Saile Pál , Sréter J. , Szántó L. , Turán P. , Wachsberger Márta
Füzet:	1926/december, 116 - 117. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1926/október: 196. matematika feladat

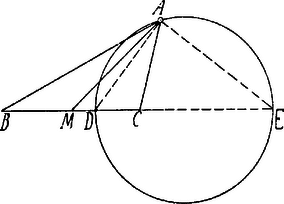
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Azon pontok mértani helye, melyekre nézve két adott ponttól való távolságuk viszonya állandó, az Apollonius-féle kör. Azon egyenesen, melyre $B C$ -t felmértük, két oly pont van, mely a kívánt feltételnek megfelel; legyenek ezek $D$ és $E$ . A $D E$ , mint átmérő fölött leírt kör bármely pontja lehet a háromszög harmadik csúcsa. Ha tehát $M$ pontból $d$ sugárral kört szerkesztünk, ez az előbbi kört a keresett $A$ , ill. $A'$ pontban metszi. De $A' B C ▵ ≅ A B C ▵$ .

Háromszöget csak akkor kaphatunk, ha az előbb meghatározott két kör metszi egymást, azaz, ha

\begin{matrix} M D < d < M E . \end{matrix}

(1)

Legyen

B C = a

és

p > q

\begin{matrix} B D : D C = p : q \end{matrix}

Mivel

B D + D C = a

, azért

B D = \frac{a p}{p + q}

\begin{matrix} M D = B D - B M = \frac{a p}{p + q} - \frac{a}{2} = \frac{a (p - q)}{2 (p + q)} . \end{matrix}

Másrészt:

B E : C E = p : q

és

(B E - C E) : B E = (p - q) : p

.
Azonban

B E - C E = a

is így

B E = \frac{a p}{p - q}

\begin{matrix} M E = B E - B M = \frac{a p}{p - q} - \frac{a}{2} = \frac{a (p + q)}{2 (p - q)} . \end{matrix}

Az (1) feltétel eszerint így írható

\begin{matrix} \frac{1}{2} (\frac{p - q}{p + q}) a < d < \frac{1}{2} (\frac{p + q}{p - q}) a . \end{matrix}

Saile Pál (kegyesrendi fg. VIII. o. Bp.)