Kezdőlap


Feladat:	168. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke Gy. , Benedek V. , Elek Tibor , Fischer Gy. , Ság M. , Wachsberger Márta
Füzet:	1926/október, 49 - 50. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Derékszögű háromszögek geometriája, Pont, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1926/május: 168. matematika feladat

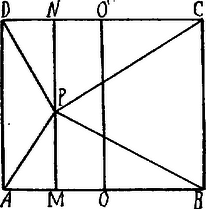
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . A $P$ ponton át húzzunk párhuzamosat pl. az $A D$ ill. $B C$ oldalakkal; legyen ez $M N$ . Ezen párhuzamost meghatározza az $M O = x$ távolság, ahol $O$ az $A B$ felezőpontja. Legyen továbbá $P M = y$ és a négyzet oldala $A B = 2 a$ .

\begin{matrix} {\bar{P A}}^{2} = {\bar{A M}}^{2} + {\bar{P M}}^{2} = {(a - x)}^{2} + y^{2} \\ {\bar{P B}}^{2} = {\bar{P M}}^{2} + {\bar{M B}}^{2} = y^{2} + {(a + y)}^{2} \end{matrix}

Ezek alapján az (1) egyenletünk ez lesz:

\begin{matrix} 2 (x^{2} + y^{2} + a^{2}) = p^{2} . \end{matrix}

(1a)

Hasonló módon látható, hogy a (2) egyenlet így alakul:

\begin{matrix} 2 [x^{2} + {(2 a - y)}^{2} + a^{2}] = q^{2} . \end{matrix}

(2a)

Az (1a) és (2a) egyenletek megfelelő tagjainak kivonása után:

\begin{matrix} 8 a y - 8 a^{2} = p^{2} - q^{2} és ebből y = \frac{8 a^{2} + p^{2} - q^{2}}{8 a} . \end{matrix}

(3)

Helyettesítsük

y

ezen értékét az (1a)-ba:

\begin{matrix} 2 x^{2} = p^{2} - 2 a^{2} - \frac{{(8 a^{2} + p^{2} - q^{2})}^{2}}{32 a^{2}}, \end{matrix}

vagy

\begin{matrix} 64 a^{2} x^{2} = - 128 a^{4} + 16 (p^{2} + q^{2}) a^{2} - {(p^{2} - q^{2})}^{2} . \end{matrix}

(4)

(4)-ből

x

-re két értéket kapunk, az

O

pontra nézve szimmetrikus helyzetű

M_{1}

és

M_{2}

pontokat.

y

-nak (3) alatti értéke mindig valós és lehet pozitív vagy negatív. De

x

értéke (4) szerint csak akkor valós, ha a jobb oldalon pozitív szám áll, esetleg zérus, azaz, ha

\begin{matrix} 128 a^{4} - 16 (p^{2} + q^{2}) a^{2} + {(p^{2} - q^{2})}^{2} ≦ 0. \end{matrix}

(5)

A baloldalon álló trinom gyökei

a^{2}

-re nézve:

\begin{matrix} a^{2} = \frac{p^{2} + q^{2} \pm \sqrt[]{{(p^{2} + q^{2})}^{2} - 2 {(p^{2} - q^{2})}^{2}}}{8} . \end{matrix}

(6)

Az (5) relacio ki lesz elégítve, ha először is a (6) értékek valósak; ennek a feltétele pedig

\begin{matrix} p^{4} - 6 p^{2} q^{2} + q^{2} ≦ 0 azaz 3 - 2 \sqrt[]{2} ≦ \frac{p^{2}}{q^{2}} ≦ 3 + 2 \sqrt[]{2} . \end{matrix}

Másodszor pedig

a^{2}

a (6) értékek között legyen!

2^{\circ}

. Azon

P

pontok mértani helye, melyekre nézve

A

és

B

ponttól való távolságok négyzetösszege állandó, oly kör, melynek középpontja az

A B

távolság felezőpontja, mint ezt az (1a) egyenlet is mutatja; ezen kör radiusa,

\begin{matrix} P O = \sqrt[]{\frac{p^{2} - 2 a^{2}}{2}} . \end{matrix}

A (2) szerint pedig

P

oly körön fekszik, melynek középpontja

C D

felezőpontja,

O'

és sugara

\begin{matrix} P O' = \sqrt[]{\frac{q^{2} - 2 a^{2}}{2}} . \end{matrix}

Ezen két kör általában két pontot határoz meg, az

O O''

egyenesre nézve szimmetrikus helyzetben. A két kör metszi egymást, ha

\begin{matrix} | \sqrt[]{\frac{p^{2} - 2 a^{2}}{2}} - \sqrt[]{\frac{q^{2} - 2 a^{2}}{2}} | < 2 < \sqrt[]{\frac{p^{2} - 2 a^{2}}{2}} + \sqrt[]{\frac{q^{2} - 2 a^{2}}{2}} . \end{matrix}

Kimutatható, hagy ezen feltétel teljesülése maga után vonja az (5) feltétel kielégítését is.

Elek Tibor (Kemény Zsigmond főreál VII. o. Bp.)