Kezdőlap


Feladat:	160. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Tibor , Beke Gyula , Bóday I. , Elek T. , Hajós Gy. , Ság Miklós , Steiner S.
Füzet:	1926/szeptember, 20. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Síkgeometriai szerkesztések, Hiperbola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1926/április: 160. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az adott pontok $A$ és $B$ adott aszimptota $m_{1}$ és a másik $m_{2}$ irányra nézve van megadva. Az $A$ és $B$ pontokat összekötő egyenes $m_{1}$ -t $K$ pontban metszi; mérjük fel $B L$ -t $A K$ -val ellenkező irányban, akkor $L$ a keresett aszimptota egy pontja, amelyen át az adott iránnyal párhuzamos egyenest húzva, megkapjuk $m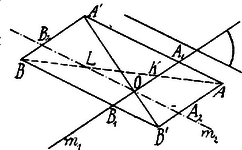_{2}$ -t.

Az ábra szerint húzzunk

A

-ból és

B

-ből az aszimptotákkal párhuzamosakat; ismeretes tétel szerint:

\begin{matrix} {\bar{A A}}_{1} \cdot {\bar{A A}}_{2} = {\bar{B B}}_{1} \cdot {\bar{B B}}_{2} . \end{matrix}

Azonban

A A_{1} = B' B_{1}

és

B B_{2} = B' A_{2}

; helyettesítve ezeket:

\begin{matrix} {\bar{B' B}}_{1} \cdot {\bar{A A}}_{2} = {\bar{B' A}}_{2} \cdot B B_{1} vagy {\bar{B' B}}_{1} : {\bar{B B}}_{1} = B' A_{2} : A A_{2} . \end{matrix}

Utóbbi aránypár azt fejezi ki, hogy

B_{1} A_{2} ∥ B A

és így

A K = A_{2} B_{1} = B L

Beke Gyula (Dugonics András fg. VII. o. Szeged)

II. Megoldás. Az

A

és

B

pontokon át az aszimptotákkal párhuzamosan húzott egyenesek oly paralelogrammát határoznak, melynek

A' B'

átlója a hyperhola középpontján,

O

-n megy keresztül.
Ugyanis

O A_{1} A' ▵ ≃ O B_{1} B' ▵

(szögeik egyenlőek); tehát

\begin{matrix} O A_{1} : O B_{1} = A_{1} A' : B_{1} B' . \end{matrix}

Az itt szereplő távolságok helyébe a velük egyenlőket helyettesítve

\begin{matrix} A A_{2} : B B_{2} = B B_{1} : A A_{1} azaz {\bar{A A}}_{1} \cdot {\bar{A A}}_{2} = {\bar{B B}}_{1} \cdot {\bar{B B}}_{2} . \end{matrix}

Bakos Tibor (szombathelyi áll. főreál. VIII. o.)

III. Megoldás. Pascal tétele szerint minden kúpszeletbe írt hatszög szemben fekvő oldalának metszéspontjai egy egyenesen ‐ a Pascal-féle egyenesen ‐ feküsznek. Ezen egyenest az adott esetben megszerkeszthetjük, mert egy érintő a görbe két pontját jelenti. Az

m_{1}

végtelenben fekvő pontja legyen

ω_{1}

és

ω_{2}

m_{2}

-é pedig

ω_{3}

és

ω_{4}

. A hat pont e szerint:

B

ω_{1}

ω_{2}

A

ω_{4}

ω_{3}

{\bar{B ω}}_{1}

és

{\bar{A ω}}_{4}

szemben fekvő oldalak, azaz

{\vec{B B}}_{2}

és

{\vec{A A}}_{1}

metszőpontja

A'

. Másrészt:

{\bar{B ω}}_{3}

és

{\bar{A \infty}}_{2}

szemben fekvő oldalak, azaz

{\vec{B B}}_{1}

és

\vec{A A_{2}}

metszőpontja

B'

. Eszerint

A'

és

B'

a Pascal egyenest határozzák meg, mely keresztül megy az

ω_{1} ω_{2}

és

ω_{4} ω_{3}

oldalak, t. i. az aszimptoták metszőpontján:

O

-n.

Ság Miklós (Kemény Zsigmond főreál. VII. o. Bp.)