Kezdőlap


Feladat:	147. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakacsi I. , Bakos T. , Bayer I. , Beke B. , Beke Gy. , Blau Kata , Bóday I. , Darvas J. , Dobroszláv L. , Elek T. , Fillinger V. , Fischer F. , Fischer Gy. , Fischer Rózsi , Füszter I. , Füszter István , Haimann E. , Hajós Gy. , Heller G. , Henkel Gy. , Hirka L. , Izr. rg. V. o. Debrecen , Kárpáti Gy. , Klein Eszter , Klein F. , Kornhauser J. , Kozma A. , Lőrincz P. , Mischung Ilona , Neufeld B. , Pál E. , Polgár L. , Rácz E. , Ság M. , Schmolka Gy. , Sebestyén E. , Séra I. , Steiner S. , Sveiczer M. , Szántó L. , Tóth István , Vámos Gy. (VI. ker.) , Wachsberger Márta
Füzet:	1926/május, 278 - 279. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1926/március: 147. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen $B C = a$ a megadott befogó és ennek vetülete $B D = p$ ; az $A C$ befogó vetülete $A D = q$ (adva); tehát 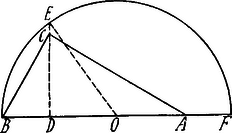$a^{2} = p (p + q)$ .

Ha az

A B

átfogót

A F = p

-vel meghosszabbítjuk és

B F = 2 p + q

fölött félkört írunk, mely

C D

meghosszabbítását

E

-ben metszi, akkor

\bar{D E^{2}} = p (p + q)

, tehát

D E = B C = a

. A

B F

átmérőhöz tartozó kör középpontja

O

egyszersmind az

A D = q

vetület felező pontja. Ezek alapján a szerkesztés menete ez lesz: az

e

egyenesre rámérjük az adott

q

vetületet; ennek egyik végpontjában (

D

) merőlegest állítunk és erre rámérjük

D E = a

-t;

q

felező pontjából,

O

-ból

O E

sugárral kört írunk, mely az

e

egyenest

B

(ill.

F

) pontban metszi, ami által

A B

, az átfogó is meg van határozva.

Füszter István (Dobó István főreál VIII. o. Eger)

II. Megoldás. Az

a^{2} = p (p + q)

egyenletben jelentse

q

egy kör átmérőjét; ha ezen körhöz a hosszúságú érintőt szerkesztünk és ezen érintő végpontjából a kör középpontján átmenő szelőt, ezen szelőnek a körön kívül fekvő szelete lesz

p

. És

p + q

a keresett derékszögű háromszög átfogója.

Tóth István (Szent Imre főreáliskola VIII. o. Esztergom)

III. Megoldás. Az

a^{2} = p (p + q)

egyenletből

\begin{matrix} p = \frac{- q \pm \sqrt[]{q^{2} + 4 a^{2}}}{2} = - \frac{q}{2} \pm \sqrt[]{{(\frac{q}{2})}^{2} + a^{2}} . \end{matrix}

A két érték közül csak az egyik, a pozitív felelhet meg. A megoldás alapján elvégezhető a szerkesztés, úgy, mint I.-ben.

Fischer Rózsi (izr. leánygimn. VII. o. Bp.)