Kezdőlap


Feladat:	116. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakos T. , Beke Gyula , Bóday I. , Elek T. , Hajós Gy. , Heller G. , Hirka L. , Izr. rg. V. o. Debrecen , Ság M. , Séra I. , Wachsberger Márta
Füzet:	1926/március, 207 - 208. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Érintőnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1926/január: 116. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az átlók $O$ metszéspontjából, az oldalakra bocsátott merőlegesek talppontjai, az ábra szerint, 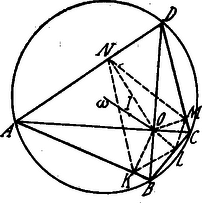$K, L, M, N$ .

A K O N

négyszög húrnégyszög, mert két szöge (

K

és

N

csúcsnál) derékszög. Ezért

O K N ∠ = O A N ∠

minthogy ugyanazon íven álló kerületi szögek. Ugyanilyen okból

O K L ∠ = O B L ∠

. Másrészt

O A N ∠ = O B L ∠

; mindakettő az

ω

kör

\hat{C D}

ívéhez tartozik.
Tehát

O K N ∠ = O K L ∠

, azaz

K O

N K L ∠

-et felezi; éppígy kimutathatjuk, hogy

L O, M O, N O

is felezik az

L, M, N

csúcsnál fekvő belső szögeit a

K L M N

négyszögnek, tehát

O

ezen négyszög oldalaitól egyenlő távolságra van és így oly kör középpontja, melyet ezen négyszög oldalai érintenek.
Ugyancsak az előbbiek alapján:

N K L ∠ = 2 O K L ∠ = 2 O B L ∠

. Hasonló módon kimutathatjuk, hogy

L M N ∠ = 2 O C L ∠ .

Eszerint

\begin{matrix} N K L ∠ + L M N ∠ = 2 (O B L ∠ + O C L ∠) = 2 \cdot 90^{0}, \end{matrix}

mert feltételeinknél fogva

B O C ∠ = 90^{0}

. Ezen megállapítás tehát azt jelenti, hogy a

K L M N

húrnégyszög.

Beke Gyula (Dugonics-András gimn. VII. o. Szeged.)

Jegyzet. Kimutathatjuk, hogy a

K L M N

köré írt kör középpontja az

ω O

egyenes felezőpontja

I

. T. i.

K

pontnak az

ω

körre vonatkozó hatványa:

\bar{K A} \cdot \bar{K B} = \bar{K ω^{2}} - r^{2}

. Másrészt az

A O B

derékszögű háromszögben:

\begin{matrix} \bar{K A} \cdot \bar{K B} = - \bar{K O^{2}} . \end{matrix}

A két kifejezés egybevetéséből

\begin{matrix} \bar{K ω^{2}} - r^{2} = - \bar{K O^{2}} ill. \bar{K ω^{2}} + \bar{K O^{2}} = r^{2} . \end{matrix}

Ha már most

ω O

felezőpontja

I

, akkor az

ω K O ▵

-nek

K I

oldalfelezőjére érvényes összefüggés alapján:

\begin{matrix} \bar{K ω^{2}} + \bar{K O^{2}} = 2 \bar{K I^{2}} + \frac{\bar{ω O^{2}}}{2} = r^{2} tehát K I = \sqrt[]{\frac{r^{2}}{2} - \frac{\bar{ω O^{2}}}{4}}, \end{matrix}

más szóval:

K I

és így

L I

stb. constans értékek.