Kezdőlap


Feladat:	115. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos T. , Beke Gy. , Elek Tibor , Heller G. , Pál E. , Steiner S.
Füzet:	1926/március, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Poliéderek súlypontja, Tetraéder magasságpontja, Feladat
Hivatkozás(ok):	Feladatok: 1926/január: 115. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 111. feladatban kimutattuk, hogy az $M$ , $S$ , $O$ pontok egy oly egyenesen feküsznek, melynek vetülete a tetraéder lapjain az illető lap Euler-egyenese.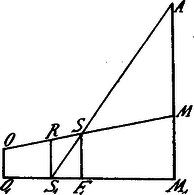
$M$ vetülete az egyik határlapon az illető lap háromszög magassági pontja, $M_{1}$ ; $O$ vetülete pedig az illető lapháromszög körülírt körének középpontja, $O_{1}$ . A tetraéder súlypontja, ha a tetraéder $A$ csúcsát a szemben fekvő lap $S_{1}$ súlypontjával összekötjük, az $A S_{1}$ egyenesen fekszik úgy, hogy a $A S : S S_{1} = 3 : 1$ . Ha már most $S$ pontot vetítjük a szóban forgó lapra, akkor $S$ pont vetülete: a határlap Feuerbach körének középpontja, $F_{1}$ lesz.

Ugyanis

A M_{1} ∥ S F_{1}

tehát

\begin{matrix} M_{1} F_{1} : F_{1} S_{1} = A S : S S_{1} = 3 : 1. \end{matrix}

Ezen aránypár az előbbi állást igazolja. Azonban

F_{1}

egyszersmind az

M_{1} O_{1}

távolság felező pontja és így

S

pont is felezi az

M O

távolságot, más szóval

O S = S M

2^{0}

. A határlap

S_{1}

súlypontjában, a határlapra emelt merőleges benne fekszik az

A M_{1} S_{1}

síkban, mely az illető határlapra merőleges; ezért az

S_{1}

pontban, a határlapra emelt merőleges az

M S

egyenest metszi egy

R

pontban. Minthogy

\begin{matrix} O R : R M = O_{1} S_{1} : S_{1} M_{1} = 1 : 2 \end{matrix}

azért bármelyik határlap súlypontjában emelt merőleges ugyanezen

R

ponton megy keresztül.

3^{0}

S R S_{1} ▵ \sim S M A ▵

. Tehát

\begin{matrix} R S_{1} : M A = S R : S M . \end{matrix}

Azonban

\begin{matrix} S R : S M = F_{1} S_{1} : F_{1} M_{1} = 1 : 3 \end{matrix}

és így

\begin{matrix} R S_{1} : M A = 1 : 3 Q. e. d. \end{matrix}

Elek Tibor (Kemény-Zsigmond főreál VIII. o. Bp. VI.)