Feladat:	95. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos T. ,  Bóday I. ,  Böhm V. ,  Fischer F. ,  Füszter István ,  Hajós Gy. ,  Heller G. ,  Kurtz G. ,  Pál E. ,  Polgár L. ,  Steiner S.
Füzet:	1926/január, 146 - 147. oldal		PDF  |  MathML
Témakör(ök):	Háromszög alapú hasábok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1925/november: 95. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Az $AMB$, $ANC$ és $ABC$ derékszögű háromszögekből: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle A{B}^2=a^2+x^2\text{...}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle }& {\displaystyle \overline{A{C}^2}=a^2+y^2\text{...}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle }& {\displaystyle \overline{B{C}^2}=\overline{A{B}^2}+\overline{A{C}^2}=2a^2+x^2+y^2\text{...}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Másrészt $BC$ oly derékszögű háromszög átfogója is lehet, melynek befogói $MN$ ill. a $B$ csúcsból húzott vele párhuzamos és egyenlő távolság ‐ továbbá $y-x$, ${}^{*}$ tehát ‐ tekintettel (3)-ra is ‐ $\begin{array}{c}{\displaystyle {\overline{BC}}^2=3a^2+{\left(y-x\right)}^2=2a^2+x^2+y^2}\end{array}$ és így $\begin{array}{c}{\displaystyle 2xy=a^2\text{<span style="font-weight: normal;font-style: normal;">ill.</span>}xy=\frac{a^2}{2}\text{...}}\end{array}$ (4) $2^{\circ }$. Legyen már most $x+y=m$. Ebben az esetben, tekintettel a (4) eredményre is $x$ és $y$ egy másodfokú egyenletnek, $z^2-mz+\frac{a^2}{2}=0$ gyökei. Ezen egyenlet gyökei valósak, ha $m^2-2a^2\geqq 0$, azaz $m\geqq a\sqrt[]{2}$. Ha valósak a gyökök, akkor pozitívok is, mert szorzatuk és összegük is pozitív. Ha $m=a\sqrt[]{2}$, $x=y=\frac{a\sqrt[]{2}}{2}$, $AB=AC=a\sqrt[]{\frac{3}{2}}$, $BC=MN=a\sqrt[]{3}$. $3^{\circ }$. Legyen $m=\frac{3a}{2}$; a diszkrimináns $m^2-2a^2=\frac{9a^2}{4}-2a^2=\frac{a^2}{4}$ és így $\begin{array}{c}{\displaystyle z=\frac{a}{2}\left(\frac{3}{2}\pm \frac{1}{2}\right);z_1=x=\frac{a}{2};z_2=y=a\mathrm{.}}\end{array}$ A prizma térfogata $V=\frac{AB\cdot AC\cdot h}{2}$. 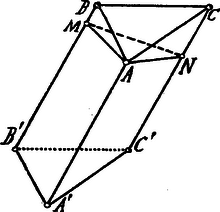$\begin{array}{c}{\displaystyle \overline{AB}=\sqrt[]{a^2+x^2}=\frac{a\sqrt[]{5}}{3};\overline{AC}=\sqrt[]{a^2+y^2}=a\sqrt[]{2}\mathrm{.}\text{<span style="font-weight: normal;font-style: normal;">Tehát</span>}V=\frac{a^{2}h\sqrt[]{10}}{4}\mathrm{.}}\end{array}$ Az $AMN▵$ felfogható, mint az $ABC▵$ ortogonális vetülete; ha ezen háromszögek síkjának hajlásszöge $\alpha$, az $AMN▵$ területe $t\text{'}$, az $ABC▵$-é $t$, akkor $t\text{'}=t\text{cos}\alpha$ és így $\text{cos}\alpha =\frac{t\text{'}}{t}$. Az előbbiek szerint $\begin{array}{c}{\displaystyle t=\frac{AB\cdot AC}{2}=\frac{a^2\sqrt[]{10}}{4}}\end{array}$ $t\text{'}$ az $AMN$ egyenlőszárú háromszög területe; ha $MN=a\sqrt[]{3}$ az alapja, akkor az erre bocsátott magasság: $\begin{array}{c}{\displaystyle \sqrt[]{A{M}^2-{\left(\frac{MN}{2}\right)}^2}=\sqrt[]{a^2-\frac{3a^2}{4}}=\frac{a}{2}\mathrm{,}}\end{array}$ és így ${\displaystyle \begin{array}{c}\hfill {\displaystyle t\text{'}=\frac{a\sqrt[]{3}}{2}\cdot \frac{a}{2}=\frac{a^2\sqrt[]{3}}{4}\text{<span style="font-weight: normal;font-style: normal;">és</span>}\text{cos}\alpha =\sqrt[]{\frac{3}{10}}}\hfill \\ \hfill {\displaystyle \alpha ={56}^{\circ }47\text{'}20\text{'}\text{'}\mathrm{.}}\hfill \end{array}}$ A prizma térfogata felírható így is: $V=t\text{'}\cdot AA\text{'}$. Eszerint ${\displaystyle \begin{array}{c}\hfill {\displaystyle t\text{'}\cdot AA\text{'}=t\cdot h\text{<span style="font-weight: normal;font-style: normal;">ill.</span>}\frac{a^2\sqrt[]{3}}{4}\cdot AA\text{'}=\frac{a^{2}h\sqrt[]{10}}{4}}\hfill \\ \hfill {\displaystyle AA\text{'}=h\sqrt[]{\frac{10}{3}}=\frac{h\sqrt[]{30}}{3}\mathrm{.}}\hfill \end{array}}$   Füszter István (áll. főreáliskola VIII. o. Eger)   Jegyzet. $m=\frac{a}{2}$ esetben nincs megoldás, mert ekkor $m<a\sqrt[]{2}$. ${}^{*}$vagy $x-y$; az eredmény szempontjából mindegy.