Feladat:	88. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bakos T. ,  Bóday I. ,  Böhm V. ,  Hajós Gy. ,  Hirka L. ,  Polgár L. ,  Steiner Sándor
Füzet:	1926/január, 140 - 141. oldal		PDF  |  MathML
Témakör(ök):	Súlypont, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1925/november: 88. matematika feladat

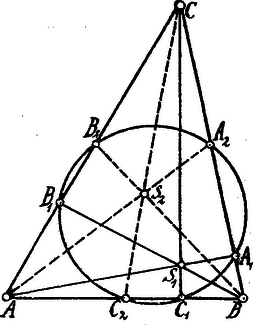
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   $1^0$. Ha az $A{A}_1$, $B{B}_1$, $C{C}_1$ egyenesek egy $S_1$ ponton mennek át, akkor a Ceva-tétel szerint $\begin{array}{c}{\displaystyle \frac{A_{1}B}{A_{1}C}\cdot \frac{B_{1}C}{B_{1}A}\cdot \frac{C_{1}A}{C_{1}B}=-1\text{...}}\end{array}$ (1) A kör szelőire vonatkozó tétel szerint: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle A_{1}C\cdot A_{2}C=B_{1}C\cdot B_{2}C\text{...}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle }& {\displaystyle B_{1}A\cdot B_{2}A=C_{1}A\cdot C_{2}A\text{...}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle }& {\displaystyle C_{1}B\cdot C_{2}B=A_{1}B\cdot A_{2}B\text{...}}\hfill & \text{(<mn>4</mn>)}\end{array}}$ (2), (3), és (4) a következő alakban írhatók: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle \frac{B_{1}C}{A_{1}C}=\frac{A_{2}C}{B_{2}C}\text{...}}\hfill & \text{(<mn>2</mn><mi>a</mi>)}\\ \hfill {\displaystyle }& {\displaystyle \frac{C_{1}A}{B_{1}A}=\frac{B_{2}A}{C_{2}A}\text{...}}\hfill & \text{(<mn>3</mn><mi>a</mi>)}\\ \hfill {\displaystyle }& {\displaystyle \frac{A_{1}B}{C_{1}B}=\frac{C_{2}B}{A_{2}B}\text{...}}\hfill & \text{(<mn>4</mn><mi>a</mi>)}\end{array}}$ Eszerint $\begin{array}{c}{\displaystyle \frac{A_{2}C}{B_{2}C}\cdot \frac{B_{2}A}{C_{2}A}\cdot \frac{C_{2}B}{A_{2}B}=\frac{B_{1}C}{A_{1}C}\cdot \frac{C_{1}A}{B_{1}A}\cdot \frac{A_{1}B}{C_{1}B}}\end{array}$ ill. a tényezők sorrendjének felcserélésével $\begin{array}{c}{\displaystyle \frac{A_{2}C}{A_{2}B}\cdot \frac{B_{2}A}{B_{2}C}\cdot \frac{C_{2}B}{C_{2}A}=\frac{A_{1}B}{A_{1}C}\cdot \frac{B_{1}C}{B_{1}A}\cdot \frac{C_{1}A}{C_{1}B}=-1}\end{array}$ azaz az $A{A}_2$, $B{B}_2$, $C{C}_2$ egyenesek is egy ponton mennek át. $2^0$. Ha $S_1$ a háromszög súlypontja, $A_1$, $B_1$, $C_1$ a háromszög oldalainak felezőpontjai. Az ezeken átmenő kör ‐ az ú. n. Feuerbach-kör ‐ átmegy a magasságok talppontjain, tehát $A_2$, $B_2$, $C_2$, a magasság talppontjai és így $S_2$ a magassági pont.   Steiner Sándor (áll. főreáliskola VII. o. Pécs)