Feladat: 61. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bakos Tibor ,  Kárteszi Ferenc 
Füzet: 1925/december, 108 - 109. oldal  PDF  |  MathML 
Témakör(ök): Súlypont, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):Feladatok: 1925/szeptember: 61. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1∘. Legyen ABC≡▵ az első, A'B'C'≡▵' a második háromszög. ▵-nek merőleges vetülele a ▵' síkján A1B1C1≡▵1. Az A, B, C csúcsokból a B'C', CA', A'B' oldalakra állított merőleges síkok metszőegyenese d, mely a ▵' síkját D1-ben döfi át.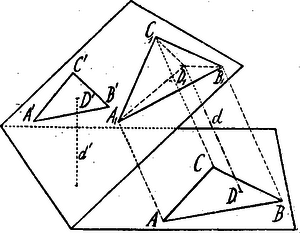

 
 

Már most pl. a C csúcsból az A'B' oldalra merőlegesen állított sík tartalmazza a CC1 vetítő sugarat is; ez a sík a CC1, C1D1 és d egyenesek síkja. Tehát A'B' merőleges ezen sík minden egyenesére:A'B'⊥C1D1. Éppígy B'C'⊥A1D1;C'A'⊥B1D1. Eszerint a ▵' és ▵1. háromszögekre alkalmazhatjuk a 48. feladat tételét (1.3. sz. 79. o.), azaz az A', B', C' pontokból a B1C1, C1A1, A1B1 oldalakra vont merőlegesek a ▵' síkjában egy D' pontban metszik egymást. Másrészt, ha A'D'⊥B1C1 akkor A'D' egyszersmind a B1C1BC síkra is merőleges,1 tehát BC egyenesre is. Ennélfogva az A'D' egyenesen lehet síkot fektetni, mely BC-re merőleges.2 De ugyanígy lehet a B'D' ill. C'D' egyeneseken át a CA ill. AB-re merőleges síkot fektetni. Tehát ez a három sík D' ponton megy át és mindegyik merőleges a ▵ síkjára 3 ezért e három sík egy egyenesben metszi egymást, d'-ben.
2∘. Ha a d egyenes az ABC▵-nek D súlypontján megy át, akkor D1 is súlypontja a ▵1-nek (mert a vetítésnél az oldalfelező súlyvonalak vetületei szintén oldalfelező súlyvonalak). De így a D' is a 48. feladat tétele szerint a ▵' súlypontja lesz, azaz d' egyenes a ▵' súlypontján megy át.
Ha ▵ és ▵' egy síkba esik, akkor a 48. feladatban vázolt helyzet, mint speciális eset jön létre.
 

Bakos Tibor (szombathelyi áll. főreál VIII. o).

1CC1 merőleges ▵' síkjára, tehát ezen sík minden egyenesére is: CC1⊥A'D'. Azaz A'D' merőleges C1B1 és CC1 egyenesekre és így az általuk meghatározott síkra is.

2L. ,,A tetraëderről'' szóló cikk 3. sz. tételét a 102. oldalon.

3Ha BC merőleges az A'D'-n átfektetett síkra, akkor minden sík, mely BC-t tartalmazza, az előbbi síkra merőleges.