Kezdőlap


Feladat:	60. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gy. , Bakos Tibor , Benedek V. , Bóday I. , Fillinger V. , Geiringer F. , Heller G. , Macz F. , Polgár Lajos , Szombathy M.
Füzet:	1925/október, 53 - 54. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1925/május: 60. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . $V (x) = \frac{4 {(x + 1)}^{3} π}{3} - \frac{4 x^{3} π}{3} = \frac{4 π}{3} (3 x^{2} + 3 x + 1)$ .
$2^{\circ}$ . Legyen már most $\frac{4 π}{3} (3 x^{2} + 3 x + 1) = \frac{4 π k}{3}$ . Egyszerűsítve a következő egyenlethez jutunk:

\begin{matrix} 3 x^{2} + 3 x + 1 - k = 0 & ... & (1) \\ x = \frac{- 3 \pm \sqrt[]{3 (4 k - 1)}}{6} & ... & (2) \end{matrix}

Valósak a gyökök, ha

4 k - 1 \geq 0

azaz

k > \frac{1}{4}

x > 0

tartozik lenni. (1) egyenletben a gyökök összege

- \frac{3}{3} = - 1

. Hogy az egyik gyök legalább pozitív legyen, a gyökök szorzatának negatívnak kell lennie. A gyökök szorzata

\frac{1 - k}{3} < 0

k > 1

.
Ha

k = 1

x = 0

3^{\circ}

y = \frac{4 π}{3} (3 x^{2} + 3 x + 1)

függvény értéke

x = \pm \infty

mellett

+ \infty

y

nem lehet zérus, mert

3 x^{2} + 3 x + 1

discriminánsa negatív. Minimuma van, ha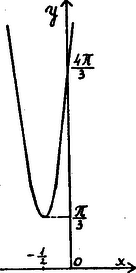

x = - \frac{3}{6} = - \frac{1}{2}

és

\begin{matrix} y_{min.} = \frac{π}{3} . Ha x = 0, y = \frac{4 π}{3} . \end{matrix}

A feladat értelmében keresnünk kell

y = \frac{4 π k}{3}

megoldásait; ezeket úgy foghatjuk fel, mint az

y = V (x)

parabola és

y = \frac{4 π k}{3}

egyenes metszéspontjaihoz tartozó abscissákat. Ezen egyenes párhuzamos az

x

tengellyel. Az ábrázolás mutatja, hogy metszéspont nem lehet, ha

y < \frac{π}{3}

azaz

\frac{4 π k}{3} < \frac{π}{3}

vagyis

k < \frac{1}{4}

; de pozitív abscissával bíró metszéspont csak akkor van, ha

\begin{matrix} y > \frac{4 π}{3,} azaz \frac{4 π k}{3} > \frac{4 π}{3} és k > 1. \end{matrix}

Polgár Lajos (egri főreál VII. o.)