Kezdőlap


Feladat:	33. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ambrus Gy. , Bakos T. , Bayer I. , Bóday I. , Bohus J. , Breitner J. , Erdélyi A. , Fischer F. , Fischer Ferenc , Geiringer F. , Horváth Sz. , Huszár L. , Macz F. , Medgyesi Ö. , Perényi A. , Polgár L. , Wessel I.
Füzet:	1925/május, 94 - 95. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Derékszögű háromszögek geometriája, Egyenes körkúpok, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1925/március: 33. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $r$ a gömb, $ϱ$ a kúp alapkörének sugara, $l$ a kúp alkotója, $m$ a gömbüveg magassága.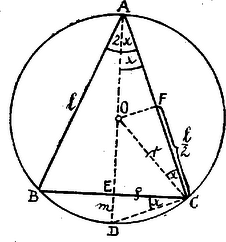

A feltétel szerint

\begin{matrix} ϱ π l = 2 r π m \end{matrix}

(1)

\begin{matrix} (2) \\ \begin{matrix} C D E & derékszögű & háromszögből & tg x = \frac{m}{ϱ}, & azaz & m = ϱ tg x ... \\ C O F & ,, & ,, & cos x = \frac{l}{2 r}, & azaz & l = 2 r cos x ... \end{matrix} \\ (3) \end{matrix}

(2)-t és (3)-t (1)-be helyettesítve

tg x = cos x

és ebből

tg x = \frac{sin x}{cos x}

, majd

cos^{2} x = 1 - sin^{2} x

helyettesítéssel

\begin{matrix} sin^{2} x + sin x - 1 = 0 \end{matrix}

(4)

(4)-ből

\begin{matrix} sin x = \frac{- 1 \pm \sqrt[]{5}}{2} . \end{matrix}

Minthogy

| sin x | \leq 1

, következik, hogy

\begin{matrix} sin x = \frac{\sqrt[]{5} - 1}{2} . \end{matrix}

Fischer Ferenc (egri áll. főreál. VII. o.)

Jegyzet. (4) egyenlet gyökei

- 1

és

+ 1

között tartoznak lenni.
Ha

f (sin x) \equiv sin^{2} x + sin x - 1

, akkor

f (+ 1) = + 1

és

f (- 1) = - 1

. Mivel e két helyettesítés értéke ellenkező előjelű, a 4) egyenletnek

- 1

és

+ 1

között csak egy gyöke lehet. (L. 2. sz. 33. oldalon c) alatt.)