Kezdőlap


Feladat:	30. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ambrus Gy. , Bakos Tibor , Benedek V. , Bóday J. , Erdélyi A. , Fischer F. , Freund P. , Geiringer F. , Heller G. , Perényi A. , Polgár L. , Schüller J. , Schäffer I.
Füzet:	1925/május, 92 - 93. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Szabályos sokszög alapú egyéb hasábok, Terület, felszín, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1925/március: 30. matematika feladat

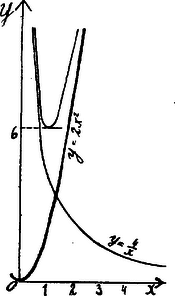
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A négyzetes oszlop felszíne: $y = 2 x^{2} + 4 x m$ . Minthogy $x^{2} m = v$ , $m = \frac{v}{x^{2}}$ helyettesítéssel $y = 2 x^{2} + \frac{4 v}{x}$ . Úgy tekinthetjük a megfelelő görbét, mint amelynek pontjaihoz tartozó ordináták az $y = 2 x^{2}$ parabola és $y = \frac{4 v}{x}$ hyperbola megfelelő pontjaihoz tartozó ordináták összege.

Tekintettel a feladatunkra,

x

csak pozitív lehet. Ha

x = 0

y = + \infty

; ha

x = + \infty

akkor

y = + \infty

; a pozitív

x

oldalon

y

nem lehet zérus. Ezen megfontolásokból is következik már, hogy a függvénynek minimuma van. Differenciálhányadosa

y' = 4 x - \frac{4 v}{x^{2}}

; második differenciálhányadosa

y'' = 4 + \frac{8 v}{x^{3}}

y' = 0

x^{3} = v

, azaz az egyenlő térfogatú négyzetes oszlopok között a kockának van legkisebb felszíne.

x^{3} = v

esetben

y'' =

= 4 + 8 = 12 > 0

; tehát ezen értéknél

y

minimum. Ha

v = 1

x = 1

értéknél

y_{{min}_{}^{}} = 6

Bakos Tibor (Áll. főreálisk. VII. o. Szombathely)