Kezdőlap


Feladat:	455. matematika ábrázoló geometria feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bauer János , Bizám György , Csáki Frigyes , Kovács Illés , Máté I. , Sándor Gyula , Steiner Iván , Szabó Béla
Füzet:	1939/február, 161. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria, Térgeometriai szerkesztések, Térelemek és részeik, Tengely körüli forgatás
Hivatkozás(ok):	Feladatok: 1938/december: 455. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A leforgatásban szerkesztünk. Az $A$ -ból húzott magasság talppontja $(D)$ a nyomvonalak távolságát felező egyenesen van 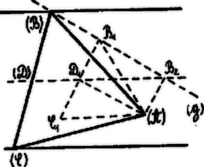$(g)$ .

Szerkesszünk egy ilyen

(A)

és

(D)

ponttal bíró egyenlőoldalú háromszöget. Könnyen bebizonyítandó, hogy ha

(D)

(g)

-t írja le, akkor

(B)

is egyenest ír le, amelynek

s

-el való metszéspontja a keresett háromszög egyik csúcsa.

Bauer János (Révai Miklós g. VII. r. o. Győr.)

II. Megoldás.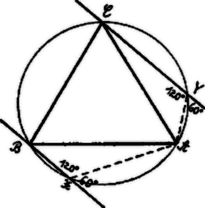

A szerkesztés az ábrából leolvasható. Mivel

\begin{matrix} A B C ∢ = 60^{\circ}, ezért A C' C ∢ = 120^{\circ}, \end{matrix}

és így a külső szög tényleg

60^{\circ}

Csáki Frigyes (Bolyai g. VIII. r. o. Budapest).

III. Megoldás.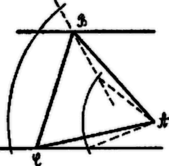

Mivel a háromszög szögei

60^{\circ}

-osak, ezért az egyik nyomvonalat

(A)

körül

60^{\circ}

-al elforgatjuk. Az így elforgatott egyenes a másik nyomvonalat a keresett háromszög egyik csúcsában metszi.

Kovács Illés (Fazekas Mihály g. VII. r. o. Debrecen.).

IV. Megoldás.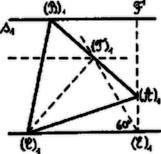

{(A)}_{1} F'

kör felezési pontjában

s_{1}

-el

∥

-t húzunk. Ennek metszéspontja az

{(E)}_{1}

-ből

s_{1}

-hez

60^{\circ}

alatt húzott egyenessel adja az egyik magasság talppontját

{(T)}_{1}

-et.
Az

{(E)}_{1} {(T)}_{1}

egyenes ugyanis mértani helye az

{(A)}_{1}

körül forgatott

60^{\circ}

-os szög egyik szárának

{(s_{2})}_{1}

-el való metszéspontjából a másik szárra ejtett merőlegessel való metszéspontjának. (1303. sz. gyakorlat.)

Steiner Iván (Toldy Ferenc g. VII. r. o. Budapest.).

V. Megoldás.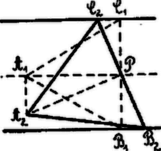

Megszerkesztjük először az

A_{1} B_{1} C_{1}

egyenlőoldalú háromszöget, majd az

| A_{2} P |

-re merőlegest húzunk. Ezen lesz

B_{2} C_{2}

. Bizonyítás:

A_{1} A_{2} P △ \sim B_{1} B_{2} P △

, mert

\begin{matrix} A_{1} ∢ = B_{1} ∢ = 90^{\circ} és A_{1} P ⊥ B_{1} P, A_{2} P ⊥ B_{2} P, \end{matrix}

azaz

\begin{matrix} α = β . \end{matrix}

De akkor

B_{1} P : A_{1} P = B_{2} P : A_{2} P

, amiről az is következik, hogy

A_{1} P B_{1} △ \sim A_{2} P B_{2} △ .

Szabó Béla (Hunyadi Mátyás honvéd r. VIII. o. Kőszeg.).