Kezdőlap


Feladat:	375. matematika ábrázoló geometria feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Komlós János , Papp I. , Sebestyén Gy.
Füzet:	1936/december, 123. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1936/október: 375. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a $C$ pontból $a$ sugárral bemetszünk a $g$ egyenesbe, a $B$ pontot kapjuk. Forgassuk le a $∣ B C ∣$ körül a háromszöget a $P_{1}$ -be. Itt megszerkeszthetjük a háromszöget: a $B C$ , mint húr fölé olyan kört szerkesztünk, melynek kerületi szöge $\frac{α}{2}$ . Ezt $B$ -ből ( $b + c$ ) sugárral metszve, kapjuk 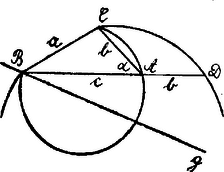$D$ -t.

Most a

B C

, mint húr fölé olyan kört szerkesztünk, melynek kerületi szöge

α

és messük e kört a

B D

-vel, kapjuk

A

-t. Forgassuk most vissza

A

-t a

B C

első vetítősíkjába s egy keresett

A B C ▵

-et kaptunk.
A hasonló háromszögek egynevű magasságai a megfelelő alapot egyenlő arányban osztják, tehát az

A'

mértani helye a

g

-vel párhuzamos

h

egyenes. Vagyis az

A

pont egyik mértani helye a

h

egyenes első vetítősíkja (

S

). A

γ

szög állandó és a

b

oldalnak első képsíkszögét jelenti, így ez az egyenes oly forgáskúp alkotója, melynek csúcsa

C

és tengelye merőleges

P_{1}

-re. E kúpfelület az

A

pont másik mértani helye. Az adott helyzetben a kúp és

S

metszésvonala hiperbola.
Mivel

D

pont kettő lehetséges, tehát kétféle

A

h

és

γ

van, tehát két kúp és két hiperbola.

Komlós János (Széchenyi István gy. g. VII. r. o. Pécs.)