Kezdőlap


Feladat:	367. matematika ábrázoló geometria feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Gárdos Pál , Gilyén J. , Illovszky Gábor , Kolostori József , Lóránd E.
Füzet:	1936/október, 58 - 59. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1936/május: 367. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen $| O B | = s$ az affinitás tengelye és az $O$ középpontú $\bar{O B} = r$ sugarú kör az ellipszis affin köre.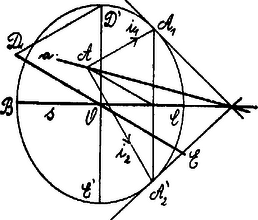

a

érintő megfelelője

A'_{1} (A'_{2})

-ben érint úgy, hogy

| A A'_{1} = i_{1}

, vagy

| A A'_{2} | = i_{2}

az affinitás iránya. Ha az ellipszis egyik átmérőjének

\bar{B C}

-t választom, akkor a konjugáltja

\bar{D E}

. A két irány

(i_{1}, i_{2})

egy ellipszist ad.

Gárdos Pál (Bólyai r. VII. o. Budapest.)

II. Megoldás. ... az affinitás iránya.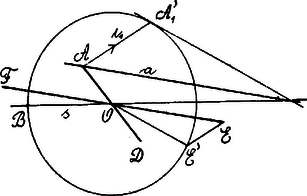

Legyen az ellipszis egyik átmérője

\bar{A D}

(A O = O D)

, akkor

\bar{E_{1} F_{1}}

a konjugáltja.

Illovszky Gábor (Kemény Zsigmond r. VII o.Budapest.)

III. Megoldás. Legyen

| O A | = s

az affinitás tengelye és

A C

az egyik ellipszis átmérő

(A O = O C)

, akkor a konjugált átmérő párhuzamos az

A

-beli érintővel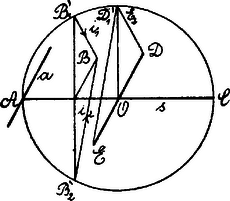

a

-val.

Így

B

-nek megfelelője

B'_{1} (B'_{2})

megszerkeszthető és

| B B'_{1} | = i_{1}

, vagy

| B B'_{2} | = i_{2}

az affinitás iránya. A két irány azonban ugyanabba az ellipszisbe viszi át az affin kört, mert

D'_{1} E'_{1} \equiv E'_{2} D'_{2}

Kolostori József (Faludi Ferenc r.VII. o. Szombathely.)