Kezdőlap


Feladat:	353. matematika ábrázoló geometria feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Brill György , Farkas Imre , Ilkovits Iván , Komlós J. , Schwarz J.
Füzet:	1936/március, 218 - 219. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1935/december: 353. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. $X$ , $Y$ , $B$ , $C$ pontok egy körön vannak, tehát egy síkban fekszenek. De $P$ az $X$ , $Y$ egyenes egy pontja, tehát a keresett kör síkja a $[P B C]$ sík. E sík a hasábot az $A' B C$ háromszögben messe.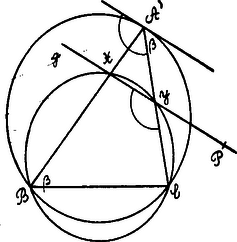

Rajzoljuk meg az

A' B C

pontokon átmenő kört és ennek az érintőjét

A'

-ben. A

P

-re illeszkedő és az érintővel párhuzamos egyenes

g

Brill György (Bólyai r. VIII. o. Budapest.)

II. Megoldás.

...

Mivel

B C X Y

húrnégyszög, ezért a szemközti szögek össszege

180^{\circ}

, amiből következik, hogy

\begin{matrix} C Y P ∢ = C B X ∢ . \end{matrix}

Farkas Imre (Szt. László rg. VII. o. Budapest.)

III. Megoldás.

...

A' B

és

A' B'

a keresett kör két szelője, tehát: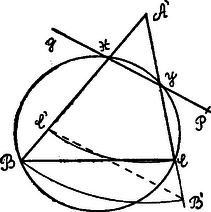

\bar{A' X} \cdot \bar{A' C} = \bar{A Y} \cdot \bar{A' B}

, ahonnan

\begin{matrix} \frac{\bar{A' X}}{A' Y} = \frac{\bar{A' B}}{\bar{A' C}}, \end{matrix}

amiből a

g

iránya megszerkeszthető.

[

\bar{A' B'}

\bar{A' B}

és

\bar{A' C'}

\bar{A' C}

Ilkovits Iván (Kemény Zs. r. VIII. o. Budapest.)