Kezdőlap


Feladat:	344. matematika ábrázoló geometria feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Brill Gy. , Csillag F. , Ilkovits I. , Komlós J. , Nagy E. , Pick György , Schreiber Béla
Füzet:	1935/december, 120. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1935/október: 344. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Illesszünk az $| A B |$ -re egy tetszőleges síkot és keressük meg itt a mértani helyet. Legyen $A O = O B = k$ és legyen egy derékszögű koordinátarendszer $X$ tengelye $A B$ , origója $O$ .

Ha a keresett mértani hely egy pontja

P

és annak koordinátái

x

y

, akkor írhatjuk:

\begin{matrix} {\bar{A B}}^{2} = {(k + x)}^{2} + y^{2} és {\bar{B P}}^{2} = {(k - x)}^{2} + y^{2} \end{matrix}

\begin{matrix} {\bar{A P}}^{2} + {\bar{B P}}^{2} = a^{2} = 2 k^{2} + 2 x^{2} + 2 y^{2}, \end{matrix}

ahonnan

\begin{matrix} x^{2} + y^{2} = \frac{a^{2}}{2} - k^{2}, \end{matrix}

A keresett mértani hely tehát a síkban kör, melynek középpontja

O

és sugara

r = \sqrt[]{\frac{a^{2}}{2} - k^{2}}

.
Ha e kört

| A B |

körül megforgatjuk, akkor az

O

középpontú és

r

sugarú gömböt kapjuk.
A feladatnak megoldása csak akkor van, ha

\begin{matrix} \frac{a^{2} - 2 k^{2}}{2} \geq 0, azaz a^{2} \geq 2 k^{2}, ill. a \geq k \sqrt[]{2} . \end{matrix}

\begin{matrix} a = k \sqrt[]{2}, akkor r = 0 \end{matrix}

és így a feladat megoldása egy pont:

O

Pick György (Bólyai r. VIII. o. Budapest)

II. Megoldás. Ha

P

a keresett mértani hely egy pontja, akkor a cosinus tétel szerint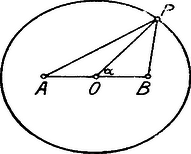

\begin{matrix} \frac{+ {\begin{matrix} {\bar{A P}}^{2} = {\bar{A O}}^{2} + {\bar{P O}}^{2} - {\bar{2 A O}}^{2} \cdot \bar{P O} \cdot cos α \\ {\bar{B P}}^{2} = {\bar{B O}}^{2} + {\bar{P O}}^{2} + 2 \cdot B O \cdot P O \cdot cos α \end{matrix}}{a^{2} = {(\frac{c}{2})}^{2} \cdot 2 + 2 {\bar{P O}}^{2}, ill. \bar{P O} = \sqrt[]{\frac{a^{2}}{2} - {(\frac{c}{2})}^{2}},} \end{matrix}

ahol

c = A B

Mivel

\sqrt[]{\frac{a^{2}}{2} - {(\frac{c}{2})}^{2}}

állandó, ezért a

P

pontok mértani helye a síkban kör, a térben gömb.

Schreiber Béla (Izraelita rg. VI. o. Budapest)