Feladat:	328. matematika ábrázoló geometria feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Brill Gy. ,  Czégé Imre ,  Fischmann Éva ,  Ilkovits Iván ,  Komlós J. ,  Lóránd E. ,  Schreiber B. ,  Steiner E.
Füzet:	1935/május, 281 - 282. oldal		PDF  |  MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1935/március: 328. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.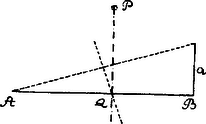   I. Megoldás. Legyen egy keresett $P$ pontnak $|AB|$-re vató vetülete $Q$, $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}{\displaystyle \text{akkor}}\hfill & {\displaystyle \overline{A{P}^2}=\overline{A{Q}^2}+\overline{P{Q}^2}}\hfill \\ {\displaystyle \text{és}}\hfill & {\displaystyle \overline{B{P}^2}=\overline{B{Q}^2}+\overline{P{Q}^2}}\hfill \end{array}}\}-}\end{array}$ és így $Q$-t a következőképen szerkesztjük meg. Egy derékszögű háromszög átfogója $\overline{AQ}$, két befogója $\overline{BQ}$ és $a$. A derékszögű $▵$ megszerkesztésére rendelkezésünkre áll az egyik befogó $\left(a\right)$ és a másik befogó meg az átfogó összege $\left(AB\right)$. Mivel $Q$ egyértelműen szerkeszthető meg, tehát minden $P$-hez ugyanazon $Q$ tartozik. A keresett mértani hely tehát egy az $|AB|$-re $\perp$ sík.   Ilkovits Iván (Kemény Zs. r. VII. o. Budapest)   II. Megoldás. Legyen $P$-nek vetülete $|AB|$-re $Q$, akkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle \overline{A{Q}^2}+\overline{Q{P}^2}-\left[{\left(AB-AQ\right)}^2+\overline{Q{P}^2}\right]=a^2}\hfill \\ \hfill {\displaystyle -\overline{A{B}^2}+2AB\cdot AQ=a^2}\hfill \end{array}}$ ahonnan $AQ={\displaystyle \frac{a^2+\overline{A{B}^2}}{2\cdot AB}}$. Minthogy ezen eredmény független a $PQ$ távolságtól, tehát a $P$ pontok mértani helye $Q$-ban $|AB|$-re $\perp$ sík.   Czégé Imre (Baross Gábor r. VIII. o. Szeged)