|
| Feladat: |
315. matematika ábrázoló geometria feladat |
Korcsoport: 18- |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bálint J. , Bartha F. , Bezzegh L. , Brill Gy. , Czégé I. , Fejér J. , Fenyő I. , Glück Gy. , Kertesi R. , Komlós J. , Krausz J. , Perényi Tibor , Pick Gy. |
| Füzet: |
1935/február,
172 - 173. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Ábrázoló geometria |
| Hivatkozás(ok): | Feladatok: 1934/december: 315. matematika ábrázoló geometria feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyenek a síkok , , , . A. keresett gömb középpontja egyenlő távolságra van mind a négy síktól.
Két síktól egyenlő távolságra lévő pontok mértani helye a két sík szögét felező (egymásra merőleges) két sík.
Három általános (egy ponton átmenő) síktól egyenlő távolságra lévő pontok mértani helye a közös pontra illeszkedő négy egyenes, amely a szögfelező sík metszésvonala és amely egyenesek a három sík által nyolc részre osztott térrész közül ‐-n haladnak át.
A keresett pont minden esetre ezen egyeneseken lehet csak. Az és pl. síkok szögfelező síkjai ezen egyeneseket egy-egy (összesen nyolc) pontban metszik. Ezek a feladat megoldásai.
Több megoldás nincs. Az és ez síkok szögfelező síkjai ugyanis egyeneseinket ugyanezen pontokban metszik. Mert ha pl. síkok szögfelező síkja az egyik egyenest más pontban metszené, akkor ez is, mint megoldás, egyenlő távol volna minden síktól és így rajta volna az síkok szögfelező síkján. De egy sík egy egyenest csak egy pontban metszhet.
A síkok különleges viszonylagos helyzete a megoldások számát megváltoztathatja. Így pl. a szabályos tetraédert (ill. a lapok meghosszabbításait) érintő gömbök száma öt. A négy szögfelező egyenes az ábrában a csúcsból indul ki. Ezek: , , , . A gömbök középpontjai az , , , és pontok, melyeket az egyenesekből az ábrában az és síkok szögfelező síkjai metszenek ki.
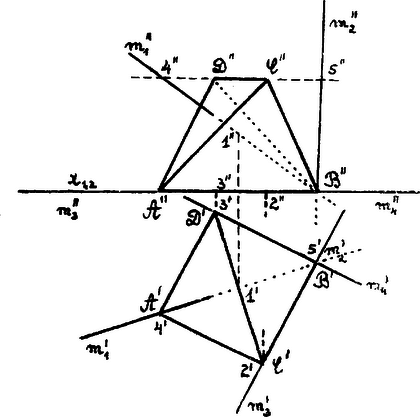
A hiányzó három középpont a -ben van, mert a -re illeszkedő első vetítő szögfelező sík párhuzamos -vel, míg a -re illeszkedő -el párhuzamos szögfelező sík párhuzamos és el.
| Perényi Tibor (Vörösmarty Mihály r. VIII. o. Budapest). |
|
|
 PDF |
PDF |  MathML
MathML 