Kezdőlap


Feladat:	257. matematika ábrázoló geometria feladat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Deutsch Ervin , Weiszfeld Endre
Füzet:	1933/április, 234 - 235. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	Feladatok: 1933/február: 257. matematika ábrázoló geometria feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szerkesszük meg először a kúpnak a koincidencia síkkal való metszésvonalát, $c$ -t. Evégből vegyünk fel egy tetszőleges $S (s_{1}, s_{2})$ síkot, melynek fővonalai egymásra merőlegesek. Ezeknek $H_{h}$ és $H_{v}$ koincidencia pontjait összekötve, a sík koincidencia egyenesét nyerjük ( $a$ ), amely $c$ -nek érintője lesz.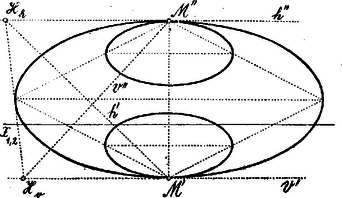

M'

tartójú

h'

és az

M''

tartójú

v''

egyenesek projektívek (képződményük kör). A két projektív sugársort a

h''

és

v'

egyenesekkel metszésbe hozva, projektív pontsorokat nyerünk, amelynek képződménye

c^{',''}

. Mivel

h'' ∥ v'

és a végtelen távoli pontok nem felelnek meg egymásnak,

c^{',''}

nem lehet parabola. Mivel a pontsorok ellentétesen projektívek, a képződmény ellipszis.
Ha

\bar{M' M''} = 2 r

, akkor

c

kistengelye

2 r \sqrt[]{2}

és merőleges

x_{1,2}

-e; nagytengelye

4 r

és párhuzamos

x_{1,2}

-vel. Ha a kúpot a koincidencia síkkal párhuzamos síkkal metsszük, akkor a metszet egy hasonló ellipszis (

d

) lesz, melynek képei

M'

-re illetőleg

M''

-re illeszkednek és

c

-hez hasonló helyzetűek.

Weiszfeld Endre (Kemény Zsigmond r. VII. o. Budapest)